讓你體會維度差異的《平面國》
上週日所寫的〈遇見克萊因瓶〉在臉書上有一千多人按讚,看起來很多人對於維度的變化很感興趣。這讓我想起《平面國》(Flatland)這本書,當年我讀這本書真有腦洞大開的感覺,值得大力推薦。
這本書的作者艾德溫·艾波特·艾波特(Edwin Abbott Abbott;沒有筆誤,他姓Abbott,中間名也是 Abbott)於1838年12月20日出生在倫敦,是位具有牧師身分的中學校長。他發表了神學、語言學等多本著作,不過流傳最廣的就是1884年出版的《平面國》。

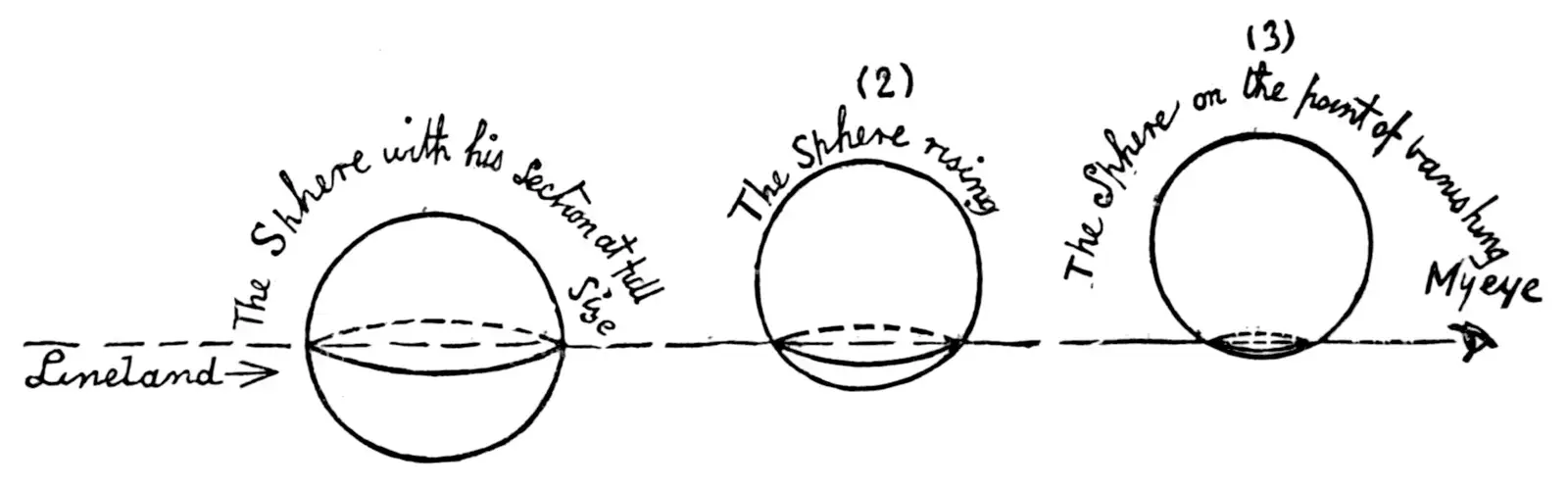
艾波特設想了平面國度中不同幾何形狀有不同地位,而且有嚴格的教條規範。書裡的主角是正方形,有一天他遇上正在穿過平面的圓球,但因為他沒有高度的概念,所以只會看到球體在平面上的切面,也就是忽大忽小的圓形。
儘管球體費盡口舌解釋,正方形仍無法想像圓球是什麼樣子,直到他被帶到三度空間,才終於理解還有第三次元,並且興奮地推論出一個點往一維移動會變成一條線,再往二維移動會變成正方形,若再向上移動就成為立方體了。於是他興奮地回到原來的平面世界後,呼籲同胞「向上!而非向北」(Upward, not Northward),擺脫一成不變的舊思維。
雖然《平面國》原意是在諷刺英國當時逕渭分明的社會階層與僵化的繁文縟節,結果由於艾波特以生動易懂的類比方式描述高低維度的差異,激發讀者對更高次元的想像,這本書反而成為影響深遠的科普書籍,從中得到靈感的包括數學家、物理學家、作家與藝術家。
以前述正方形為例,向上移動就成為立方體,那麼,立方體往第四次元移動呢?雖然我們無法直接想像超立方體的樣子,但可以用類比的方式思考:既然立方體在二維平面的展開圖是十字架狀的六個正方形,那麼超立方體在我們這個三度空間的展開就應該是由立方體組成的立體十字架(想像十字架狀的平面展開圖向上下移動)。超現實畫家達利那幅基督釘在超立方體上的畫《受難》(Corpus Hypercubus),便是基於這個思路;這也是電影《星際效應》最後,男主角在書架背後的五次元空間所呈現的樣貌。

為了向《平面國》這本書致敬,《星際效應》電影導演諾蘭特地將它放在男主角的書架上。此外,天文學家卡爾·薩根也曾在科普的電視節目中拿它來討論以;物理學家兼科普作家加來道雄在《穿梭超時空》書中除了引述《平面國》的內容,還闡述更多不同維度交會時的神奇例子。
科幻與科普作家艾西莫夫讚譽《平面國》是「如何感受維度概念的最佳入門」。的確如此,如果莫比烏斯環、克萊因瓶讓你對不同維度有興趣,這本書或有助於你跳脫思考框架。
參考資料:
- Edwin Abbott Abbott – Wikipedia
- 《平面國》,Edwin Abbott Abbott 著,賴以威 譯,魔酒出版