12月1日—幾何學的哥白尼

歐幾里得於西元前300年所寫的《幾何原本》，堪稱影響最深遠的數學鉅著，全書僅用五個公設就推導出各種幾何學定理。所謂公設就是不證自明的事實，不過其中第五公設（也就是如今所稱的平行公設）不像其它公設那麼顯而易見（註），讓數學家們不禁猜測：這或許並不是公設，而是可以用前四個公設推導出來的定理。

無數數學家因此費盡心思想要加以證明，但都以失敗告終，第五公設就這麼一直矗立著，沒想到兩千一百年之後，竟被俄羅斯數學家羅巴契夫斯基（Nikolai Lobachevsky）撼動了，他指出第五公設既非不證自明的公設，甚至不是顛撲不破的定理。

羅巴契夫斯基1792年12月1日出生於俄羅斯，7歲喪父後，家中更加貧困，所幸他獲得獎學金才得以進入喀山大學（Kazan University）就讀。第二年校方聘請來自德國、亦是「數學王子」高斯好友的數學家巴爾特斯（Johann Bartels）擔任數學系主任，羅巴契夫斯基在他的指導下，從此踏上數學生涯，留在喀山大學任教。

羅巴契夫斯基也嘗試推導第五公設，但同樣無功而返，不過他不像前人就此認命接受，反而轉念懷疑也許第五公設根本就無法用四條公設推導出來，並企圖證明這一點。

他決定採用歸謬法，先設定第五公設是錯的，也就是：「過線外一點，不只有一條直線與原來直線不相交。」然後用這否定命題和其它四條公設展開推演，應該會產生邏輯矛盾的結果，代表第五公設確實可由其它公設得證；相反地，倘若並未出現邏輯矛盾，就代表第五公設獨立於四條公設之外，無法用四條公設推導出來。

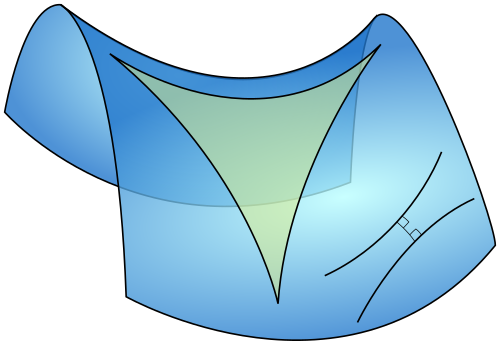
結果雖然產生一連串有別於歐氏幾何的古怪定理，但所有定理和邏輯推導都能保持內在的一致性和正確性，不會產生任何矛盾。羅巴契夫斯基於1826年發表論文時，將這全新的幾何系統稱為「虛幾何」，如今我們則以他的姓氏稱之為「羅式幾何」，或是「雙曲幾何」，因為它適用於馬鞍狀的雙曲平面。

不過當時學界的反應相當冷淡，畢竟他的理論挑戰了大家習以為常的歐氏幾何，也違背人們對空間和形狀的常識性理解。羅巴契夫斯基豪不氣餒，六年後寫就更完整的論文交予科學院審查，結果得到更猛烈的反撲，飽受各界的抨擊與嘲諷。其實高斯私下也曾涉獵非歐幾何的研究，但或許就是擔心引起軒然大波而未發表，他也只在給朋友的信中對羅巴契夫斯基的論文大加讚譽，卻未予公開聲援。

羅巴契夫斯基於1846年因健康因素被學校解雇，幾年後雙眼又逐漸失明，無法行走，最終在1856年抑鬱而終，享年63歲。就在他過世兩年前，黎曼也發表了「球面幾何」，非歐幾何才終於開始獲得學界認可。半世紀後，非歐幾何更是成為愛因斯坦提出廣義相對論的數學基礎。羅巴契夫斯基這位「幾何學的哥白尼」，不僅發起對歐氏幾何的革命，也成就了物理學的革命。

註：歐幾里得原本是寫：「如果一條直線與另外兩條直線相交，同側的兩個內角和若小於兩個直角，那麼這兩條直線如果無限延長，將在兩個內角和小於兩個直角的這一側相交。」後來才被數學家重新表述為較簡明的：「給定一條直線，通過此直線外的任何一點，有且只有一條直線與之平行。」