3月31日—現代哲學與數學的開創者
1618年，笛卡兒來到荷蘭南部一個城鎮，加入駐守當地的軍隊。有一天他走到市集閒逛，經過廣場的公佈欄時，目光不禁被上面的一張佈告所吸引──那竟然是一道數學題目？！
-
-
3月30日—這一天，決定了高斯將成為「數學王子」
1796年的3月30日，將滿19歲的高斯解決了自歐幾里得以來，高懸兩千年無人能解的難題：如何將圓十七等分？完成此一足以列入史冊的成就，讓他終於下定決心，要將一生奉獻給數學。
-
3月3日—最先認清無限大的人
面對這些無限大衍生的種種矛盾，數學家普遍認為無限只能當作一種概念，不能加以計算或比較大小。數學王子高斯就嚴肅表示：「我反對將無限量看成真實的實體來運用，這在數學之中是永遠不被允許的。無限只是一種說法而已。」直到不信邪的德國數學家康托爾出來挑戰長久以來的禁忌，用集合論照出無限大的真正原形。
-
二千三百年前如何知道太陽有多大？
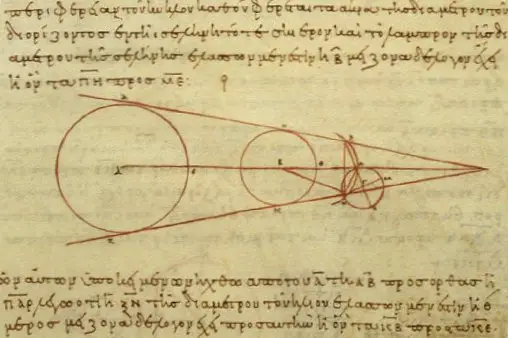
我在2月19日那篇〈哥白尼冥誕〉中提到西元前二百多年的希臘學者阿里斯塔克斯（Aristarchus of Samos）推算出太陽的大小是地球的300倍。有讀者問道：他是怎麼推算的？ 首先，阿里斯塔克斯在月全食時，從地球的影子剛好遮住一半月表時開…
-
1月7日—「無限猴子定理」是怎麼來的？
你應該聽過「無限猴子定理」：讓無限隻猴子在打字機上隨機按下字母，只要時間夠久，一定能產生任何特定的文句，例如莎士比亞全集。 根據這個定理，看似再不可能的事情，只要機率不是零，都有可能發生。但你知道嗎？這個比喻的原始出處所要表達的完全不是這個意思。 最早提出這個比喻的人，是出生於1871年1月7日的法國數學家博雷爾（Ém…
-
《魷魚遊戲》中的無限遞迴
《魷魚遊戲2》中有這麼一幕：男主角知道三角形圖案的椪糖最簡單，胸有成竹地挑了之後，打開卻發現是極為複雜的三角形圖案。 《魷魚遊戲》第二季第四集出現的謝爾賓斯基三角形。 這個圖案可不是製作單位隨便弄的，而是有所本，稱為「謝爾賓斯基三角形」，由波蘭數學家謝爾賓斯基（Wacław Sierpinski）在1915年所提出。產…
-
從質數到二進位計算機——萊布尼茲的創見
1676年底，三十而立的萊布尼茲離開待了四年的巴黎，返回德國。在巴黎期間，他已構思出微積分此一全新的數學方法，卻沒有公開對外發表，回國後他仍將之暫擱一旁，反而研究起質數來了。 他先在1678年2月發表一篇論文，指出任何大於5的質數減去1或5，一定能被6整除（這也可以表述成「任何大於3的質數都可以寫成6k ± 1」的形式…
-
每個孤獨的梅森質數，都伴隨一個完美的數
質數是孤獨的，它的因數就只有1和它自己，不像6還有2和3，15還有3和5，但質數卻再也沒有其它因數，就像一個沒有任何朋友的小孩，只能抱著1這個布娃娃，自己玩耍。 2p-1這種形式的梅森質數當然也是如此。不過，如果把-1挪個位置，移到指數p的後面，再和自己相乘的話，奇蹟就出現了：2p-1 x (2p-1) 會是個完美的數…
-
不發一語卻滿堂喝采的數學演講
上一篇〈追尋更大的質數〉提到法國神父梅森在1644年提出一系列質數，認為將它們代入Mₚ = 2ᵖ-1，所得出的答案也是質數，結果其中有些數字他搞錯了，例如1876年法國數學家盧卡斯便證明了M₆₇不是質數。 既然M₆₇是合數，那麼它的因數是什麼…
-
