從質數到二進位計算機——萊布尼茲的創見
1676年底，三十而立的萊布尼茲離開待了四年的巴黎，返回德國。在巴黎期間，他已構思出微積分此一全新的數學方法，卻沒有公開對外發表，回國後他仍將之暫擱一旁，反而研究起質數來了。 他先在1678年2月發表一篇論文，指出任何大於5的質數減去1或5，一定能被6整除（這也可以表述成「任何大於3的質數都可以寫成6k ± 1」的形式…
-
-
每個孤獨的梅森質數，都伴隨一個完美的數
質數是孤獨的，它的因數就只有1和它自己，不像6還有2和3，15還有3和5，但質數卻再也沒有其它因數，就像一個沒有任何朋友的小孩，只能抱著1這個布娃娃，自己玩耍。 2p-1這種形式的梅森質數當然也是如此。不過，如果把-1挪個位置，移到指數p的後面，再和自己相乘的話，奇蹟就出現了：2p-1 x (2p-1) 會是個完美的數…
-
不發一語卻滿堂喝采的數學演講
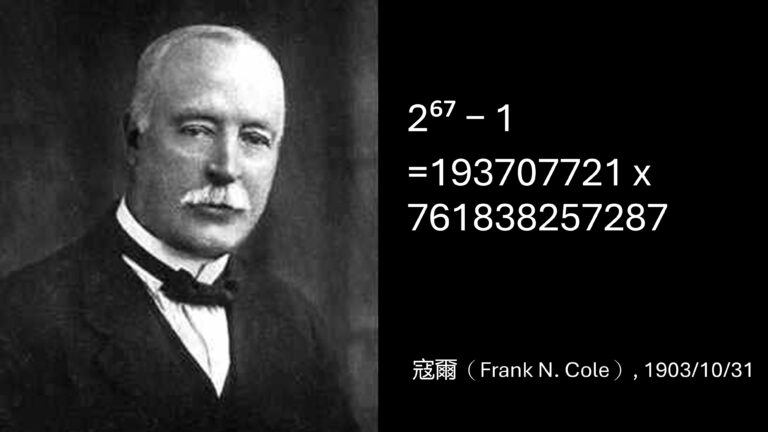
上一篇〈追尋更大的質數〉提到法國神父梅森在1644年提出一系列質數，認為將它們代入Mₚ = 2ᵖ-1，所得出的答案也是質數，結果其中有些數字他搞錯了，例如1876年法國數學家盧卡斯便證明了M₆₇不是質數。 既然M₆₇是合數，那麼它的因數是什麼…
-
-
四處漂泊，卻發表最多論文的數學家
前天是一代宗師歐拉的忌日，他是史上最多產的數學家。巧的是，史上發表最多論文的則是今天忌日的艾狄胥（Paul Erdős），他發表的論文數量多達1,525篇。雖然這些並非全部都由他自己獨力完成，但相對而言，他能與511位數學家合作，也代表他所觸及的領域之廣、投入的時間之多，實在無人能及。 艾狄胥於191…
