如果你在兩千多年前,如何知道地球大小?
今天是夏至,「至」不是到來的意思,而是代表極至;這一天是一年之中,太陽與地面垂直的最北之處(也就是北回歸線),再來太陽就又慢慢南移了。因此夏至是北半球整年度白晝最長的日子,而位於北回歸線的物體到了正午時刻,就會沒有影子。
二千二百多年前的一個夏至,古希臘的埃拉托斯塞尼 (Eratosthenes, 276 BC-194 BC) 就利用這點得知了地球的周長。

夏至正午的影子
埃拉托斯塞尼的出生地在現今的利比亞地區,他長大後到雅典接受教育,精通數學、天文學、地理學,還是位詩人。西元前245年,他被托勒密國王任命為當時規模最大的亞歷山卓圖書館館長,約莫五年後,他想到了測量地球大小的方法。
埃拉托斯塞尼從文獻記載得知,位於亞歷山卓南方的塞耶尼 (Syene) 有一口水井,每年的夏至正午,水井深處的水面正好映照出完整的太陽,也就是說太陽此刻恰好與地面垂直。
夏至的正午在亞歷山卓的物體還是有影子的,代表陽光是斜射過來的,與物體的頂端有個夾角。假設射到地球的太陽光線是平行的,而地球正圓形,那麼這個夾角就會等於亞歷山卓到塞耶尼這段圓弧對應到地心的圓心角;只要知道角度多少,就能從兩地距離依比例推算出地球的周長。
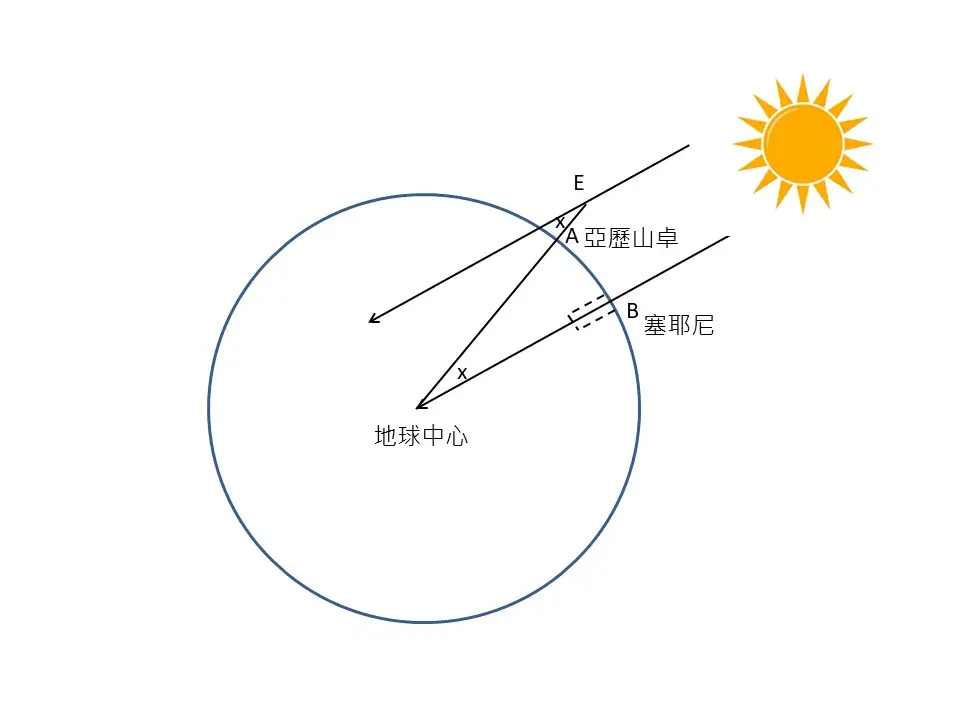
埃拉托斯塞尼測出夾角是 7.2 度,代表圓心角相當於 360 度的 1/50;而塞耶尼距離亞歷山卓 5,000「斯塔德」(stadia,古希臘距離單位),因此地球周長等於 25 萬斯塔德。(後來埃拉托斯塞尼又把地球周長調整成 25 萬 2 千斯塔德,或許是因為這個數目被 10 以內的自然數都能整除。)
斯塔德在不同地區所定義的長度各不相同,若按托勒密王國的一般標準相當於 185 公尺,但也有學者將當時測量的距離與現今比較,換算出來的是 157.7 公尺。若是前者,25 萬斯塔德相當於 4 萬 6 千公里;後者則是 3 萬 9 千公里,與實際地球周長四萬公里誤差只有 2.5%。
就算是拿 4 萬 6 千公里這個數字來比較,誤差 15% 就高了點,但這仍無礙於埃拉托斯塞尼所展現的高超抽象思考能力。以當時的技術,絕對不可能實際測量出地球周長(遑論大部分人仍認為地球是平的),但他卻能將自然現象化約為簡潔的幾何模型,不用蠻力,也無需深奧的理論,就解開這看似無解的問題,堪稱是最能呈現科學之力與美的代表作之一。
But……,埃拉托斯塞尼是怎麼量出 7.2 度的?目前有各種說法,而最常見的就是立竿見影。
實際操作遇到的問題
幾年前我曾與泛科學的雷雅淇策畫,在夏至這天效法埃拉托斯塞尼算出地球周長。當天賴以威伉儷帶著竿子在北投,廖英凱去嘉義北回歸線處,頂著烈陽等正午時刻一到,開始進行測量。
問題來了,原來竿子的黑影並沒有截然分明的邊界,因此該如何認定影子的長度就一定會產生誤差。當然,竿子如果越長,誤差比例就越小,所以在某些故事版本裡,埃拉托斯塞尼並不是用竿子,而是測量方尖碑的影子,感覺上似乎比較有道理。
但是,已知直角三角形的底(影子)跟高(竿子或方尖碑)就能反推出斜邊與高的夾角,這三角學是埃拉托斯塞尼死後才出生的希帕克斯 (Hipparkhos,190 BC – 120 BC) 發明的,所以也不可能用這個方法算出。
碗型日晷?
《如何幫地球量體重》這本書的作者認為是用希臘時期常見的一種碗型日晷 (Scaphe)。晷針的影子比較清楚,然後埃拉托斯塞尼只要測量弧型影子的長度,以及碗的完整圓周周長,就可算出影子是圓周的 1/50,不用知道角度。不過這個前提是碗型日晷要做得很渾圓,否則誤差也會很大,我不確定當時是否有這樣的技術能力。

比較可能的應該還是要測量夾角。怎麼測呢?我想像的是從影子末端拉一根細線到晷針頂端,然後拿塊繃平的薄紗,描繪出晷針與細線,就可量測出夾角占全圓的比例。當時還沒有量角器,比較簡單的方式可能是:一直將夾角複製貼上,最後湊滿一個圓剛好是 50 個。
但猜想畢竟只是猜想,希望以後有新的文獻出土,記載埃拉托斯塞尼究竟是怎麼測出來的。