1997年初的某一天,一位科學記者來到AT&T實驗室,訪問資訊科學部門主管葛立恆。在記者的探詢下,這位已過花甲之年的數學家挪開角落的彈跳桿與獨輪車,拿出五顆球,坐在辦公椅上將球逐一拋到空中。只見他雙手不斷接住落下的球再往上拋,還不時變換球的運動軌跡,他一邊向記者表示辦公室的天花板不夠高,不然拋接六顆球也沒問題。

哈哈,天花板夠高的話,或許葛立恆還能表演高難度的彈翻床特技體操呢!只是為什麼一個數學家會如此鍾情雜耍特技?
流轉與翻轉
葛立恆於1935年出生在加州的塔夫特(Taft),這是因附近油田而形成的小城鎮,父親就在油田工作。由於父親常換工作地點,全家也跟著搬遷,以致葛立恆從未在同一所學校待超過一年半;不過從小就展現數學天賦的他,卻也因此常在轉學時跳到更高年級。
15歲時,葛立恆拿到福特基金會的獎學金,高中沒有畢業就直接進入芝加哥大學。他一入學就被雜耍特技的社團吸引,投入練習的時間比讀書還多,很快成為拋接球與彈翻床高手,還被學校派去高中巡迴招生,以示芝加哥大學生活多采多姿。
由於福特基金會的獎學金只給三年,葛立恆無法繼續負擔芝加哥大學學費,便轉到加州大學柏克萊分校的電機系就讀,結果他上了萊默(Derrick H. Lehmer)教授的數論課後,激發起對離散數學的興趣。
一年之後,將滿20歲的葛立恆擔心自己會中籤入伍,索性於1955年主動加入空軍,派駐到阿拉斯加擔任通訊專員;由於值勤時間是在夜間,他還可利用白天到阿拉斯加大學讀物理系。四年之後,葛立恆取得大學文憑,再返回柏克萊讀研究所,指導教授正是萊默教授;為了賺取生活費,他還到馬戲團客串翻跳床表演。1962年,葛立恆取得數學博士學位,隨即到位於紐澤西的貝爾實驗室上班。
摯友與愛妻
1963年,葛立恆到科羅拉多州參加數論研討會,中場休息時,看見已頗有名氣的艾狄胥在打桌球。他停下腳步看了一會兒,艾狄胥突然問他要不要比一場。葛立恆平常就有在打桌球,自忖打敗這個年已半百的老傢伙應易如反掌,便立刻答應,沒想到結果竟被痛宰!葛立恆回家後立刻買了球桌,並加入桌球俱樂部勤加練習、不斷比賽,最後拿到紐澤西州的冠軍;這是他第二個州冠軍頭銜,之前他在柏克萊時,就曾得到加州彈翻床比賽第一名。
葛立恆和艾狄胥不打不相識,自此成為他一生的摯友。艾狄胥長居美國卻沒有自己的家,葛立恆特地在家中為他留個房間,讓他隨時可以來住。艾狄胥不時自掏腰包發獎金給世界各地的數學家,也都是由葛立恆代為打理,久而久之竟成了熟悉各國貨幣匯率的專家。
葛立恆也和艾狄胥一起發表了很多篇論文,其中有項猜測便以他們兩人為名,直到2003年才獲得證明。不過葛立恆最常合作的對象是1974年取得博士學位後,和他成為貝爾實驗室同事的金芳蓉,他們共同發表的論文有上百篇,佔了葛立恆全部論文的四分之一。他們不只是學術上的夥伴,兩人於1983年結婚後,成為白頭偕老的終身伴侶。

都是演算法
他們夫婦倆共同發表的論文以圖論為主,尤其是在「拉姆齊定理」(Ramsey’s theorem,註)方面;其實金芳蓉個人的第一篇論文就是關於拉姆齊定理,而葛立恆則於1971年將拉姆齊定理推及高維空間時,從某個問題得出一個非常非常巨大的「葛立恆數」,曾列入金氏世界紀錄「嚴格數學證明中最大的數」。
(葛立恆數大到難以想像;假設每個氫原子可寫進10¹⁰⁰個數字,那麼用填滿整個可觀測宇宙的所有氫原子,也還寫不完葛立恆數,而且還差非常遠。)
葛立恆完全不是那種只埋首於數字的數學家,他積極參與數學推廣與社群活動,曾先後當過美國數學學會(American Mathematical Society)與美國數學協會(Mathematical Association of America)的主席。除了純數學,他對通訊與計算機科學也有所貢獻,不但在AT&T實驗室擔任首席科學家,退休後也成為加州電信與資訊科技研究所的首席科學家。對了,他還跨界到曾於1972年擔任國際雜耍者協會主席。
不過在葛立恆眼中,這三者本質上有共通之處,他曾表示「雜耍基本上是一種基於演算法的活動,需要規劃明確的程序步驟來達成各種表演,這其實是計算機科學和離散數學中非常典型的演算法。」或許是享受雜耍中的數學型態與結構,他始終不斷學習各種雜耍特技。
1996年艾狄胥過世,令葛立恆更深覺人生苦短。他向來訪的記者表示,想在繪圖紙畫上100格*100格、共一萬個格子,每天進辦公室就劃掉一格……。2020年7月6日,葛立恆因肺病過世,享年84歲;如果他真的做了那張表格,大約只剩1,500格沒劃,他應該會滿意自己的精彩一生吧?
註:拉姆齊定理主要是說任何系統中一定存在某種程度的規律,例如一場宴會如果有6位賓客,其中一定至少有3個人彼此都認識或彼此都不認識;這可以表示成R(3,3)=6。那麼如果要確保4個、5個,或更多人都彼此認識或都不認識,需要有多少賓客呢?
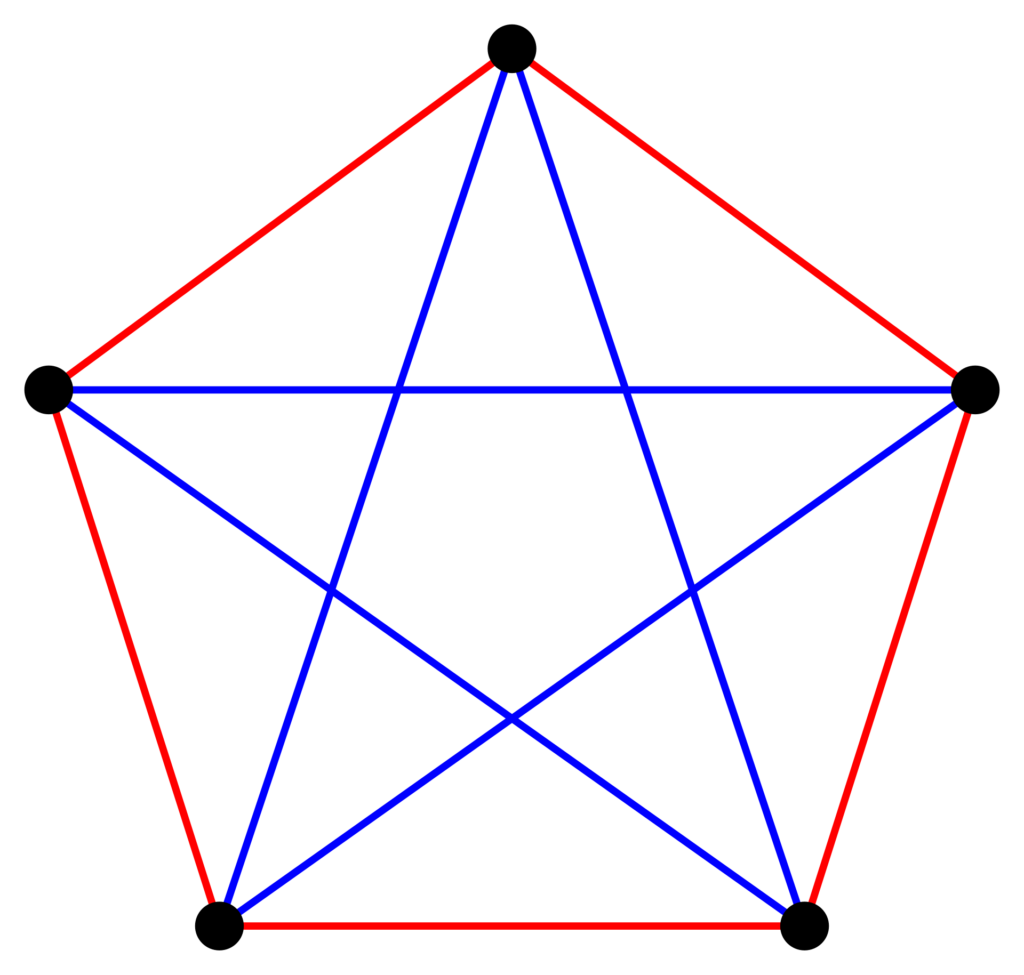
這種問題沒有公式可以直接算出,只能將賓客當成多邊形的頂點,然後兩點之間都以直線相連,用藍色和紅色分別代表認識或不認識,再判斷是否存在每邊都同色的三角形、四邊形、五邊形、……。
問題是每增加一個頂點,邊長著色的可能變化就會急遽增加,不可能一一檢查。艾狄胥生前曾如此比喻:「如果外星人要求我們算出R(5,5),否則要摧毀我們,那麼我們應該集結所有電腦與數學家之力,努力算出答案。 但如果他們要求的是R(6,6),那我們還是攻擊外星人好了。」
參考資料:
- Ronald Graham – Wikipedia
- Ronald Graham (1935 – 2020) – Biography – MacTutor History of Mathematics (st-andrews.ac.uk)
- Sci Am Profile Of Ron Graham (archive.org)
- 數學傳播 | 有朋自遠方來-專訪Ronald Graham 教授 (sinica.edu.tw)
- Too big to write but not too big for Graham | plus.maths.org
- From 1,000,000 to Graham’s Number — Wait But Why
- Ron Graham Obituary · IJA (juggle.org)










