追尋更大的質數
很多人應該知道幾天前這則新聞了:一位前NVIDIA工程師發現迄今所知最大質數:
2136279841-1
它共有41,024,320 位數,如果比照之前有本印出π的前100萬位數的書,每頁1萬個數字的話,那麼這個質數可以印成41冊。
前一個最大質數是2018年發現的282589933-1,「只能」印成25冊,再前一個則是2017年發現的277232917-1,兩者相差160萬位數,這次一下子多了1,600萬位數,無疑是很大的躍進。
梅森質數
你或許有注意到這幾個質數都是2n-1的形式(而且n都是質數),難道質數都長這樣嗎?當然不是,不過目前所發現特別大的質數,很多都是如此。這最早是17世紀的法國神父梅森(Marin Mersenne)所提出,因此2p-1(p代表質數)這種形式的質數便稱為「梅森質數」。他在1644年列出下列幾個數字:
2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257
認為將它們代入Mp = 2p-1,得出的都會是質數(M2=3, M3=7, M5=31,……)。
當時只知道到19都是質數無誤,但31之後就是梅森自己的猜測了,結果直到1772年,大數學家歐拉才證明M31是質數,然後再過一百年,M127才被證明是質數。至於M67和M257,梅森猜錯了,它們並非質數,另一方面,他反而漏掉了61, 89, 107這幾個會得出梅森質數的數字。
當數字越來越大時,要驗證是否為質數就是這麼困難,尤其是在只能用紙筆計算的年代。法國數學家盧卡斯(Édouard Lucas)於1857年,以15歲之齡發明一種較快速的檢驗法,不需一一試除質因數,仍然花了19年的時間才證明有39位數的M127是質數。若繼續靠人工計算,可能窮極一生也找不到更大的質數,想要再有所突破,只能等待電腦出現了。
電腦驗算
二次大戰後,英美紛紛開發基於馮紐曼架構的可程式化數位電腦,英國曼徹斯特大學的「曼徹斯特一號」也是其中之一。負責開發測試程式的圖靈便在1949年中寫了一支程式,用來逐一驗算梅森質數,不過受限於曼徹斯特一號的硬體規格,在發現更大的質數之前便終止測試了。

雖然圖靈的程式未發現新的質數,卻從此開啟了用電腦尋找質數的時代。1951年,劍橋大學用EDSAC電腦發現180×(M127)2+1 也是質數。第二年,美國數學家羅賓遜(Raphael Robinson)用國家標準局的電腦,在一年內就發現五個梅森質數:M521、M607、M1279、M2203、M2281,並證明到22303-1為止,再無其它梅森質數。
隨著電腦運算能力的提升,更多質數陸續被找到,但隨著數字越來越大,質數也越來越稀少,到了1994年,也不過又多發現17個更大的質數(其中16個是梅森質數)。有鑒於此,美國電腦科學家沃特曼(George Woltman)於1996年初發起「網際網路梅森質數大搜尋」(Great Internet Mersenne Prime Search,簡稱GIMPS)計畫,讓有興趣的人下載程式到個人電腦,集群體之力一起驗算梅森質數。
不到一年,GIMPS即找到下一個梅森質數,之後每隔一、兩年就有斬獲,迄今已發現18個梅森質數;目前所知最大的前七個質數,全都是出自GIMPS。
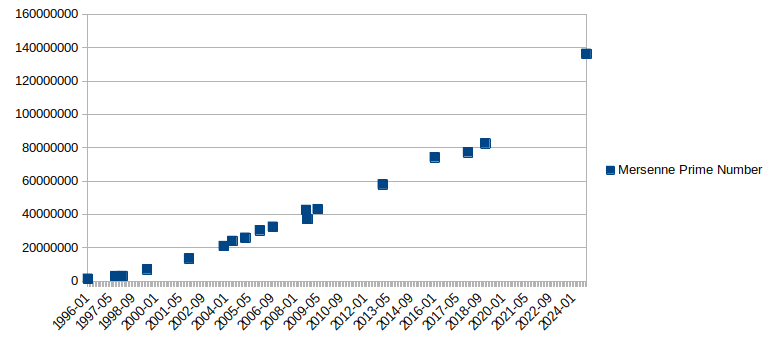
值得一提的是,這次前NVIDIA工程師杜蘭(Luke Durant)運用GIMPS的方式和以往截然不同。之前透過GIMPS發現的17個梅森質數,用的都是個人電腦,但杜蘭是將分布在17個國家的24個資料中心串連起來,成為有數千顆GPU的雲端超級電腦。結果成效斐然,原本搜尋更大質數已六年沒有進展,而他只花了一年時間就取得成果,而且是大幅度的躍進。
找到這麼大的質數有什麼用?嗯,目前是沒有實際用處,但對杜蘭而言,這達成了他想證明的:除了用來打造AI,GPU也可用於數學和科學的基礎研究;而對GIMPS的參與者而言,這項成就也彰顯了他們過去的貢獻。
其實人類文明的重大進展往往奠基於原本看似無用的知識,就像古希臘學者絕想不到質數會成為現代加密法的基礎,誰知道追尋更大的質數未來會派上什麼用場?
參考資料