Category 數學

《瑪格麗特戀習題》與哥德巴赫猜想

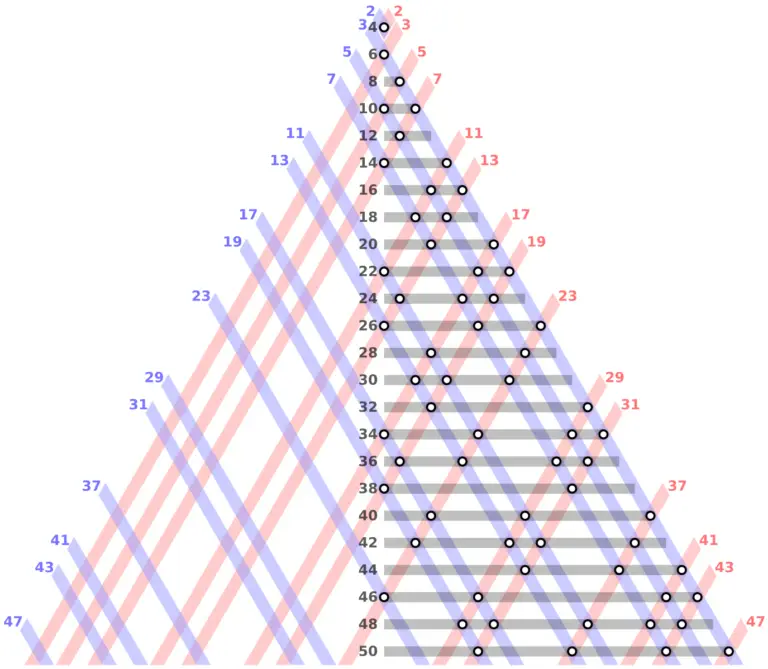
昨天看到有人發現π一直到小數點後16位數若是17張麻將牌，恰恰就是可以胡牌的排型（如下圖）。 剛好我上週看了一部法國電影 《瑪格麗特戀習題》(Marguerite’s Theorem)，描述一位原本放棄數學的女研究生，正是從麻將中獲得靈感，讓她重新振作，企圖攻克高懸近三世紀的數學難題——哥德巴赫猜想（Goldbach’s conjecture，也稱為「強哥德巴赫猜想」），也就是「任何一個大於2的偶數都可以寫成兩個質數之和」（例如12 = 5+7；40 = 3+37 或 11+29 、 17+23 ）。 提出此一猜想的哥德巴赫於1690年3月18日出生於普魯士公國的柯尼斯堡（Königsberg，二次大戰後歸蘇聯所有），他曾於1713年赴牛津大學接受牛頓指導，1725年受聘前往俄國新成立的聖彼得堡科學院。同時獲聘的還有後來提出「白努利定律」的白努利（Daniel Bernoulli）及其哥哥，兩年後在白努利的推薦下，年僅20歲的天才數學家歐拉（Leonhard Euler）也來到聖彼得堡科學院。 1728年，彼得二世成為俄國沙皇，立即將哥德巴赫攬為家庭教師，隔年彼得二世把宮廷從聖彼得堡遷往莫斯科，哥德巴赫也隨之前往。從此他開始和留在聖彼得堡的歐拉書信往返討論數學問題，時間長達35年，共有196封信。其中1742年6月7日的這封信中，哥德巴赫寫下一個猜想： 「任何由兩個質數相加而成的整數，都可以寫成任意多的質數加總，直到所有項都是基本單位為止。」 所謂的基本單位是1，這是因為當時1仍被當成質數。他在信中就舉4、5、6為例，例如4 = 1+3 = 1+1+2 = 1+1+1+1。 哥德巴赫似乎是寫完才又突然想到，而在信紙的邊緣處寫下第二個猜想： 「任何一個大於2的整數都可以寫成三個質數之和」。 然後寫說如果這個猜想成立，第一個猜想自然也成立。（現在1不算質數，這個猜想如今便改寫成「任何一個大於5的奇數都可以寫成三個質數之和」，也稱為「弱哥德巴赫猜想」。） 歐拉於6月30日回信給哥德巴赫，提醒他之前曾猜想任何一個大於2的偶數都可以寫成兩個質數之和，還說這如果成立，就會得出他信上的第一個猜想；歐拉接著寫道：你的第二個猜想其實也會隨之成立（也就是只要證明了強哥德巴赫猜想，弱哥德巴赫猜想自然得證）。歐拉最後說自己相信「任何一個大於2的偶數都可以寫成兩個質數之和」是完全確定的定理，雖然他無法證明。 連天才數學家歐拉都做不到，可見要證明看似簡明的哥德巴赫猜想其實非常困難。事實也是如此，之後一百多年無數數學家競相投入，卻絲毫沒有進展，大數學家希爾伯特因此在1900年的國際數學家大會中，將之列為最重要的23個數學問題之一。 這座令人不知從何攀爬的高峰終於在1920年代出現突破口。英國數學家哈代（Godfrey Hardy）和李特伍德（John Littlewood）所發展出在單位圓上做路徑積分的「圓法」，證明了在廣義黎曼猜想成立的前提下，每個足夠大的奇數都能表示為三個質數之和，而幾乎每個足夠大的偶數都能表示成兩個質數之和。祕魯數學家賀夫各特（Harald A. Helfgott）最終在2013年用圓法證明了10的29次方以上的奇數都能寫成三個質數相加，以下的奇數再用電腦一一驗算也都成立。雖然不是純然用數學推導，但弱哥德巴赫猜想總算是證明為真了。 但圓法在強哥德巴赫猜想上始終無法取得更大進展，不過挪威數學家布朗（Viggo Brun）在1920年利用「篩法」，證明任何足夠大的偶數都能拆成兩個不超過9個質數相乘的數字相加，提供了另一條攻克哥德巴赫猜想的路徑。 布朗的成果簡稱為「9+9」，之後三十餘年，許多數學家繼續加以縮減為「7+7」、「6+6」、「5+5」、「4+4」、「3+4」、「3+3」、「2+3」，但這樣相加的兩個數字都不是質數，代表仍有巨大的鴻溝。1962年，28歲的中國數學家潘承洞完成「1+5」的證明，也就是1個質數加上最多由5個質數相乘之數，跨出了一大步。很快地，「1+4」、「1+3」的證明陸續出現；1966年，中國數學家陳景潤又證明了「1+2」，離終點似乎只差一步，但這條路就此卡住，至今仍無法跨越。 《瑪格麗特戀習題》這部電影中，女主角瑪格麗特從麻將牌型是2張和3張的組合，竟悟得證明強哥德巴赫猜想的另一條蹊徑，如此戲劇化的安排不知是否因為麻將是中國國粹，而隱含對陳景潤等人致敬之意？至於瑪格麗特最終是否成功取得聖杯，由於電影仍在上映中，我就先不透露了。…

關於「愛因斯坦地磚」的補充

沒想到我在〈2023年十大科學新聞〉介紹的「愛因斯坦地磚」，竟然吸引那麼多人的關注。不過由於還有其它幾則科學新聞要同時並列，所以我只做了概要的介紹，有些重要關鍵就略而不提。這裡我就進一步補充說明，讓有興趣的人可以知道大概的來龍去脈。 今年64歲的史密斯是在2022年11月發現後來暱稱為「帽子」的13邊形，它看起來奇形怪狀，但其實是由8個一模一樣的箏形所組成，而這箏形是將一個正六邊形均分成六等份而來（如下圖）。 史密斯印了一堆「帽子」出來，在桌上一個個拼接起來，拚了很久，發現都沒有出現重複的圖案，不禁猜想莫非真的被他找到了愛因斯坦地磚？不過自己這樣土法煉鋼也不是辦法，誰知道範圍更大後會不會開始出現某種規律？ 加拿大滑鐵盧大學的卡普蘭教授（Craig Kaplan）是密鋪（Tessellation，也就是用幾個幾何圖形不留縫隙地鋪滿整個平面）的專家，他還自己寫了密鋪的電腦程式。於是史密斯寫email給卡普蘭，請他幫忙驗證帽子是不是愛因斯坦地磚？ 卡普蘭用電腦跑了半天也都沒看到週期性，不過就算讓電腦跑一萬年，也無法就此證明這就是愛因斯坦地磚，必須從數學上加以證明才行。卡普蘭在2023年1月找了兩名對密鋪也有研究的幫手，一位是專精凸幾何的史特勞斯（Chaim Goodman-Strauss）教授，另一位是兼具組合數學與軟體開發專長的邁爾斯（Joseph Myers）博士。 2月時，他們已經找到方法證明帽子的確可以鋪滿平面而不具週期性，就在卡普蘭著手寫成論文時，邁爾斯又有了新發現。 原來去年12月史密斯曾email另一個像是烏龜的13邊形給卡普蘭，問他這個會不會也是愛因斯坦地磚？「烏龜」也是用箏形組成，不過比帽子多了兩片（如下圖）。卡普蘭心想帽子都還沒搞定，哪有閒工夫再研究另一個烏龜，何況有可能半世紀來數學家都找不到的愛因斯坦地磚，一個業餘玩家在兩個禮拜內就發現兩個嗎？便將它暫擱一旁。 如今帽子的證明搞定了，卡普蘭繼續忙著寫論文，得空的邁爾斯覺得不妨檢視一下烏龜，結果他從兩者的共通性發現另一種方法，可以證明帽子和烏龜都是愛因斯坦地磚。這不但強化了他們預備發表的論文，而且第二種證明方法未來也可用來檢驗其它幾何形狀。 他們四人的論文發表後立刻轟動學界，不過熱烈迴響之中卻也伴隨著一項質疑。帽子和烏龜固然能沒有規律地密鋪整個平面，卻需摻雜著一些反面，也就是本身的鏡像（如下圖）。雖然在數學上，鏡射和平移、旋轉一樣，都被視為並未改變幾何形狀，因此帽子和烏龜的確算是愛因斯坦地磚，但還是有許多人提出質疑，認為應該不能用到鏡像才算數。 這時史密斯又想出另一個形狀，看起來像是烏龜和帽子的混合體，也是13邊形，不過這次的組成不是箏形（如下圖）。這個形狀也可以做為愛因斯坦地磚，更讚的是完全不需要用到反面。 只不過有個問題，如果搭配反面，反而可以排出規律的圖案（如下圖）。然而若按嚴格定義，愛因斯坦地磚只能有非週期性的排法，不允許還有規律的排法。 他們四人再次合作，很快地將找出方法，將直線的邊修改為曲線，如此便無法用正反面排出規律圖案，但仍能非週期性地密鋪整個平面（如頁首）。他們於五月發表論文，這個暱稱為「幽靈」(spectres) 的愛因斯坦地磚終於不會有人質疑了。 參考資料：

2023年十大科學新聞

一、發現「愛因斯坦地磚」 用地磚鋪滿一個平面有各式各樣的拚接方式，最簡單的當然是用正方形、正三角形或正六邊形拼接，但這樣太過單調無趣，因此自古數學家們就嘗試用兩種以上的不同幾何形狀來鋪滿平面，尤其伊斯蘭學者更是在建築中發揮得淋漓盡致。 不過這樣雖然大大增加了美感，卻仍有明顯的規律性，同樣的圖案不斷往四周延伸，也就是所謂的「週期性重複」。那麼是否有「非週期性重複」的拼接方法？ 數學家在1964年找到了這種拼接方法，不過需用到20,426種地磚，後來又簡化到103種形狀。因為對黑洞的研究而獲頒2020年諾貝爾物理獎的潘洛斯（Roger Penrose），於1974年又進一步發現兩種地磚形狀，可以非週期性地鋪滿整個平面。這令人不禁要追問：是否可能減少到只用一種地磚？由於德文的「一塊石頭」(ein stein) 和「愛因斯坦」(Einstein)同音，因此這種假想中的地磚也叫「愛因斯坦地磚」。 大部分的數學家直覺上都認為不可能有愛因斯坦地磚，不過退休的印刷技師史密斯（David Smith）在2022年發現一種13邊形，這種形狀和其鏡像的組合（也就是地磚的正面和反面）似乎可以不重複地完全鋪滿。但他無法加以證明，於是求助於另外三位數學家。2023年3月，他們四人發表論文證明史密斯的確找到了愛因斯坦地磚。 緊接著在5月，他們又發現不需要鏡像就能不重複地鋪滿平面的方法，而且這個13邊形還可以再變形出一系列的愛因斯坦地磚。誰能料到，長久以來普遍認為不可能的數學問題，就這麼解決了，而且破解的還是一位把數學當閒暇興趣的業餘玩家。 二、成功從太空將電力傳回地球 太陽能是取之不竭的乾淨能源，不過由於日夜交替與天候因素，太陽能板所能產生的電力終究有無法突破的上限。布署在太空的太陽能板就一天24小時都會受到日照，如果能將所產生的電力送回地球，不就可以大幅改善能源問題？ 這個科幻作品中早就有的構想如今終於證明是可行的。2023年6月1日，加州理工學院的團隊宣布他們成功從地球軌道上的「太空太陽能演示器一號」(Space Solar Power Demonstrator-1, 簡稱SSPD-1)，將太陽能轉換的電能，透過微波傳送到地面上的指定位置。 雖然這項「微波陣列傳輸電力低軌道實驗」(Microwave Array for Power-transfer Low-orbit Experiment, 簡稱MAPLE) 還只是概念驗證，要提供足夠電力仍有許多工程問題要克服，但這已為太空太陽發電邁開重要的一步。 三、室溫超導體成真？ 2023年7月27日，韓國科學技術研究院的團隊發表論文，宣稱發現一種以銅摻雜鉛磷灰石的合成材料”LK-99”，在常溫常壓下就有超導現象，也就是零電阻以及完全抗磁性。這則新聞一出立即轟動全球，因為如果屬實，那麼從能源、交通、醫療，乃至各種電子用品及電氣設備，都將產生革命性的躍進，徹底改變人類的科技文明。 世界各地的學術機構立即進行實驗加以驗證，結果發現LK-99並不是超導體，只是具有一定的抗磁性。韓國團隊宣稱的重大突破終究是烏龍一場，室溫超導體這個聖杯還有待科學家們繼續追尋。 四、探測器首度在月球南極成功著陸 2023年8月23日，印度的「月船3號」(Chandrayaan-3) 成功在月球南極軟著陸。由於月球的兩極地區崎嶇不平，又有巨大的隕石坑，較不容易著陸，因此之前美國、蘇聯及中國的登月任務都是選擇較為平坦的中低緯度區域。如今印度不僅成為第四個成功登月的國家，更是史上首度在月球南極登陸。 印度之所以選擇較困難的月球南極，是因為2008年發現那裏的隕石坑底下蘊藏豐富的水冰。水不僅可以供太空人飲用，經電解處理成氧氣和氫氣後，還可分別供太空人呼吸及作為火箭燃料，是建立月球基地的必要資源。而且隕石坑周邊高聳的山峰一直受到陽光照射，宛如永晝，在峰頂上架設太陽能板，便能為月球基地提供源源不絕的電力。 接下來其它國家當然也將陸續進行登陸月球南極的太空任務，尤其這次印度全部才花費7,500萬美元，倘若藉此低廉的成本為其它國家提供登月服務，勢將改變原本由少數強國把持的生態，展開新一輪的太空競賽。 五、人類祖先曾瀕臨滅絕 現在分布全球的人類都是源自五萬年前至二十萬年前，陸續走出非洲的智人；他們取代了更早離開非洲的尼安德塔人，卻也因為混血而把尼安德塔人的部分基因留傳了下來。 若更往前推，智人和尼安德塔人在70萬年前有共同的祖先，當然也算是我們人類的祖先。根據刊登於2023年8月31日出刊的《科學》期刊的一篇論文，人類的祖先在90萬年前曾急遽銳減，僅1.3%倖存下來，繁衍的個體數量最少時只有1,280個，而且接下來 11萬7千年都沒有再擴增。 這個數字實在令人觸目驚心，在那麼長的時間裡，倘若有嚴重一點的危險或災難，人類祖先就從此滅絕了。這也讓人不禁省思，高達98.7%的人類祖先之所以消失，肯定是環境變遷所致，如今人類造成的地球暖化導致氣候變遷的問題日益嚴重，我們豈能不積極挽救，以免重蹈瀕臨滅絕的覆轍。 六、NASA回收探測器採集的小行星樣本 小行星探測器「歐塞瑞斯號」（OSIRIS-REx）於2016年發射升空，2020年10月降落在小行星貝努（Bennu）表面，成功採集了170克的樣本，隨後飛返地球。…

12月22日—能看見無限的人

1934年，已經67歲的數學大師哈代（G. H. Hardy）面對年輕數學家艾狄胥（Paul Erdős）的提問：「您自認對數學的最大貢獻是什麼？」哈代腦海中浮現的不是任何數學公式或定理，而是一張永難忘懷的面孔，於是他毫不猶豫的回答：「發現拉馬努金！」隨即再補上：「與他的合作是我人生中的一個浪漫的意外。」哈代不禁嘴角上揚，思緒已飄向從前……。 那是1913 年 1月，哈代收到一封來自印度的信，一個作記帳工作的印度青年自稱沒上過大學，但利用閒暇時間自學數學，得出了一些定理，請他過目指教。所附的數學定理洋洋灑灑寫滿九張信紙，多是各種無窮級數的等式，絢麗璀璨令人目眩。 哈代從未見過這樣的數學式，宛如在他熟悉的數學森林裡突然冒出許多新品種的花朵，令人不禁懷疑是人工拼湊的偽造品，例如： 哈代把信擱在一旁，本想置之不理，但愈想愈覺得它們不可能是假的，因為沒有人可以如此憑空想像捏造出這些式子。他約了劍橋大學的同僚李托伍德（J. E. Littlewood）一起檢視這些定理，最後兩人判定這位名不見經傳的拉馬努金根本是位具有卓越創造力的天才數學家。著名哲學家也是數學家的羅素（Bertrand Russell）當時也在劍橋，他給女友的一封信就寫道：「在餐廳裡我發現哈代與李托伍德欣喜若狂，因為他們自認發現了第二個牛頓──一個年薪20磅的印度職員。」 拉馬努金於1887年12月2日出生在當時仍是英國殖民地的印度，11歲就問倒寄宿在他們家的兩名大學生，13歲就自己發現許多三角學定理。16歲時他從圖書館借了一本數學書籍，裡面收集了五千多條數學定理和公式，但沒有詳細證明與說明，拉馬努金埋頭鑽研，第二年就開始自己衍生出新的定理。然而拉馬努金一直沒有跟任何學界接觸，不知道應該要嚴謹地證明他所發現的定理，甚至還自創一些數學符號，難怪他寄給哈代的數學式宛如奇花異草。 事實上，他的洞見宛如天啟，他曾說： 「我曾在睡夢中有過不尋常的經驗。有一片彷彿由流動的血液形成的紅色光幕。我觀察著它，突然，一隻手開始在光幕上寫字，我立刻全神貫注。那隻手寫了一些橢圓積分，它們牢牢地印在我的腦海裡。我醒來後，立刻將它們寫在紙上。」 哈代安排拉馬努金於1914年來到劍橋後，才赫然發現拉馬努金對當代數學的無知，於是他從頭教導拉馬努金如何以正統的方式表述數學，同時盡量不去阻礙他的創意。拉馬努金在1915年間發表了39篇論文，1916年拿到博士學位，1918年入選為英國皇家學會會士，同年十月成為第一位獲選為三一學院院士的印度人。 表面看起來，拉馬努金在英國的生活似乎一帆風順，但其實他早就身心俱疲。他抵達英國那年就爆發第一次世界大戰，他因宗教信仰吃素，但戰時食物配給有限，以致營養不良。他工作過勞又不適應英國寒冷的天氣，加以思鄉心切卻因戰爭無法回印度，終於在1917年病倒了。在兩年的療養過程中，拉馬努金先被以為是胃潰瘍，後來被診斷為肺結核；期間換過八位醫生、五間療養院。 有一次哈代坐計程車去療養院探望他，不經意提到：「今天搭計程車的車牌號碼是1729，這個數字沒啥意思，希望不是不祥之兆。」拉馬努金答道：「不會啊，這是個很有趣的數字，它是可以用兩種方法表達為兩立方和的數字中最小的（即 1729 = 13 + 123，另外也等於 93 + 103）。」 1919年2月，一次世界大戰結束三個月後，拉馬努金終於可以回印度，但返鄉後健康狀況仍未好轉，最後於隔年四月過世，享年33歲。哈代得知後大受打擊，因為拉馬努金去世前兩個月還以愉悅的語氣寫信給他，報告他新的研究成果。哈代深感悲傷與遺憾的表示對拉馬努金虧欠許多，與他共事的五年當中，拉馬努金一直都是他創意與靈感的泉源。 拉馬努金留下來的筆記本中仍然藏有很多尚待挖掘的寶藏。除了對於純數學本身的貢獻，他的一些定理已廣泛地被應用在各種不同領域，包括統計力學、粒子物理、密碼學、弦論等等。每個知道他的人都不由得設想：如果拉馬努金不是如此英年早逝，他那具有神秘直覺的大腦還會為人類埋下多少超越時代的種子。 參考資料：

從五次方程式到橢圓函數——讓數學家忙上五百年的天才

上一篇〈破解三次方程式的博學奇才〉講到，數學家很早就發現二次方程式的根式解（也就是將方程式中的係數透過四則運算與開根號解出所有的根），但之後歷經數百年卻一直對三次方程式束手無策。這個難題直到十六世紀中期才終於被義大利數學家卡爾達諾（Girolamo Cardano）破解，而他的弟子費拉里（Lodovico Ferrari）也跟著找出四次方程式的根式解。 受此激勵，數學界普遍相信再來找出五次方程式的根式解應該指日可待，不料將近三個世紀過去了，每個試圖挑戰的數學家都鎩羽而歸，就連萊布尼茲、歐拉、拉格朗日、高斯等大師在多方嘗試後也都知難而退。沒想到，挪威一位高中生竟然宣稱找到了五次方程式的解法。 阿貝爾（Niels Henrik Abel）於1802年8月5日出生，當時挪威還屬於丹麥—挪威聯合王國，1814年瑞典入侵後，挪威被迫獨立出來，成為臣服於瑞典的聯盟；阿貝爾的父親原是牧師，獲選為國會議員。 阿貝爾自小在家由父親親自教導，直到13歲上中學才離家住校，怎奈遇到脾氣暴戾的老師，學業成績一落千丈。三年後，父親因得罪議長而被迫離開政壇，竟開始酗酒，全家生計逐漸陷入困頓。就在阿貝爾陷入內外交迫之際，來了一位年輕的數學老師何姆波（Bernt Holmboe），宛如天使般適時伸出援手。 在何姆波的循循善誘下，阿貝爾迅速展露數學天分。何姆波列出書單，讓阿貝爾自學歐拉、高斯、拉格朗日等大師的著作，並且幫他申請獎學金，讓他無後顧之憂。到了高中最後一年，何姆波已經無法再給予阿貝爾任何指導，更令他訝異的是，阿貝爾竟交出五次方程式的解法。 一個高中生完成無數大師都做不到的事？這也太匪夷所思！但何姆波仔細看過卻又找不到錯誤，他唯恐是自己能力有限，便轉寄給兩位大學教授，請他們確認。結果他們也挑不出毛病，於是又寄給丹麥的數學家迪根 (Carl Ferdinand Degen) ，請這位北歐最頂尖的數學家審閱，看是否能直接在期刊上發表。迪根一時也看不出有什麼問題，但為求謹慎，他請阿貝爾用五次方程式的實例實際演示一遍，阿貝爾這時才發現自己的解法有錯。迪根不願見他繼續浪擲數學天分，便建議他將心力轉向橢圓積分這個新的數學領域。 1821年阿貝爾高中畢業，進入大學就讀，之前幫他檢查五次方程式解法的那兩位教授相當惜才，不但資助他的學費，還於1823年安排他到丹麥參訪。阿貝爾就在這裡認識了未來的未婚妻克莉絲汀。 阿貝爾雖然聽從迪根的建議研究橢圓函數，但五次方程式一直在他心中縈繞不去。從丹麥回到挪威後，他開始思考或許五次方程式不像二次、三次、四次方程式那樣存在根式解，這正是為什麼無數人前仆後繼卻都無功而返。於是他不再尋找解法，相反地，他要證明五次方程式並不存在根式解。 其實義大利醫生魯菲尼 (Paolo Ruffini) 早在1799年就已提出這個證明，並陸續將論文分送出去。但畢竟他只是個業餘數學家，很難讓人相信他能發現250年來諸位數學巨擘都沒看到的事實。加上他的證明極為複雜，得花時間才能研判正確與否，結果收到的數學家大多沒有回應，等到他1822年過世後，更沒人知道這篇論文的存在，當然阿貝爾也不知情。（不過魯菲尼的證明並不完備，因為他用了一項假設，卻未證明此一假設為真。） 經過幾個月的努力，阿貝爾終於成功完成證明，為高懸近三百年的難題畫上句點。但由於經濟拮据，為了節省印製論文的費用，阿貝爾將完整證明濃縮成短短六頁，裝訂成冊後，於1824年寄送給當代知名的數學家。結果他也和魯菲尼當年一樣受到忽視，寄出去的論文全都石沉大海，像高斯收到後根本連信封都沒拆開。即使有人打開來看，也因他濃縮後的證明過於精簡以致艱澀難懂，懶得仔細研讀。 阿貝爾本想藉此劃時代的發現謀得教職，無奈天不從人願，於是他1825年大學畢業後，申請獎學金出國留學。他先到德國柏林，在這裡和一位工程師克列爾 (August Crelle) 成為好友。克列爾完全臣服於阿貝爾的天才，第二年創辦世上第一份數學期刊後，連續刊登了阿貝爾多篇論文，終於讓他開始獲得注目。 1826年阿貝爾轉赴巴黎，埋首幾個月完成一篇關於超越函數的論文後，滿懷期待地將論文寄給法國科學院。當時科學院的秘書傅立葉將論文交給勒讓德（Adrien-Marie Legendre）和柯西（Augustin-Louis Cauchy）審閱，但前者老態龍鍾，無力了解，後者高傲自負，根本沒打開看。這篇論文三年後被德國的雅可比 (Carl Jacobi) 發現，這位日後躋身大師之林的青年數學家讚嘆道：「或許是我們這個世紀最重要的發現。」無奈為時晚矣。 阿貝爾苦等幾個月都沒有消息，又得了肺結核健康惡化，只好先到德國投靠好友克列爾。阿貝爾抱病完成一系列橢圓函數的文章後，思鄉心切，克列爾勸他留下來擔任數學期刊的編輯，但他婉拒了，於1827年返回挪威。找不到工作的阿貝爾只能當家教掙錢；貧病交迫中，他赫然發現雅可比也發表了橢圓函數的論文，於是日以繼夜地趕工，交出了橢圓函數的加法定理、雙週期性，以及橢圓積分的反演等重大發現。 1829年4月6日，阿貝爾終於不敵病魔，病逝於床上，臨終前愧疚地要求大學好友照顧始終不離不棄的未婚妻。兩天後，遠在德國的好友克列爾尚未聞其死訊，欣喜地寫信通知阿貝爾已獲柏林大學聘任為數學教授。一年之後，法國科學院才於1830年6月將象徵最高榮譽的數學論文大獎，頒給阿貝爾與雅可比兩人。 從21歲破解五次方程式的謎題，到26歲英年早逝，阿貝爾在短短五年內就做出許多影響深遠的貢獻，如今以他為名的數學定理或名詞超過30個，法國數學家埃爾米特 (Charles Hermite) 也說：「阿貝爾留給數學家的，夠他們忙上五百年。」只可惜對於他的肯定與榮耀都來得太晚，倘若他能早日脫離貧病交迫，不知還會留下多少重大成果。 （2002年，挪威政府為了紀念阿貝爾兩百年誕辰，設立阿貝爾獎，比照諾貝爾獎，每年頒獎鼓勵傑出的數學家。） 參考資料：