沒想到我在〈2023年十大科學新聞〉介紹的「愛因斯坦地磚」,竟然吸引那麼多人的關注。不過由於還有其它幾則科學新聞要同時並列,所以我只做了概要的介紹,有些重要關鍵就略而不提。這裡我就進一步補充說明,讓有興趣的人可以知道大概的來龍去脈。
今年64歲的史密斯是在2022年11月發現後來暱稱為「帽子」的13邊形,它看起來奇形怪狀,但其實是由8個一模一樣的箏形所組成,而這箏形是將一個正六邊形均分成六等份而來(如下圖)。

史密斯印了一堆「帽子」出來,在桌上一個個拼接起來,拚了很久,發現都沒有出現重複的圖案,不禁猜想莫非真的被他找到了愛因斯坦地磚?不過自己這樣土法煉鋼也不是辦法,誰知道範圍更大後會不會開始出現某種規律?

圖片來源:Quantum Magazine
加拿大滑鐵盧大學的卡普蘭教授(Craig Kaplan)是密鋪(Tessellation,也就是用幾個幾何圖形不留縫隙地鋪滿整個平面)的專家,他還自己寫了密鋪的電腦程式。於是史密斯寫email給卡普蘭,請他幫忙驗證帽子是不是愛因斯坦地磚?
卡普蘭用電腦跑了半天也都沒看到週期性,不過就算讓電腦跑一萬年,也無法就此證明這就是愛因斯坦地磚,必須從數學上加以證明才行。卡普蘭在2023年1月找了兩名對密鋪也有研究的幫手,一位是專精凸幾何的史特勞斯(Chaim Goodman-Strauss)教授,另一位是兼具組合數學與軟體開發專長的邁爾斯(Joseph Myers)博士。
2月時,他們已經找到方法證明帽子的確可以鋪滿平面而不具週期性,就在卡普蘭著手寫成論文時,邁爾斯又有了新發現。
原來去年12月史密斯曾email另一個像是烏龜的13邊形給卡普蘭,問他這個會不會也是愛因斯坦地磚?「烏龜」也是用箏形組成,不過比帽子多了兩片(如下圖)。卡普蘭心想帽子都還沒搞定,哪有閒工夫再研究另一個烏龜,何況有可能半世紀來數學家都找不到的愛因斯坦地磚,一個業餘玩家在兩個禮拜內就發現兩個嗎?便將它暫擱一旁。

如今帽子的證明搞定了,卡普蘭繼續忙著寫論文,得空的邁爾斯覺得不妨檢視一下烏龜,結果他從兩者的共通性發現另一種方法,可以證明帽子和烏龜都是愛因斯坦地磚。這不但強化了他們預備發表的論文,而且第二種證明方法未來也可用來檢驗其它幾何形狀。
他們四人的論文發表後立刻轟動學界,不過熱烈迴響之中卻也伴隨著一項質疑。帽子和烏龜固然能沒有規律地密鋪整個平面,卻需摻雜著一些反面,也就是本身的鏡像(如下圖)。雖然在數學上,鏡射和平移、旋轉一樣,都被視為並未改變幾何形狀,因此帽子和烏龜的確算是愛因斯坦地磚,但還是有許多人提出質疑,認為應該不能用到鏡像才算數。
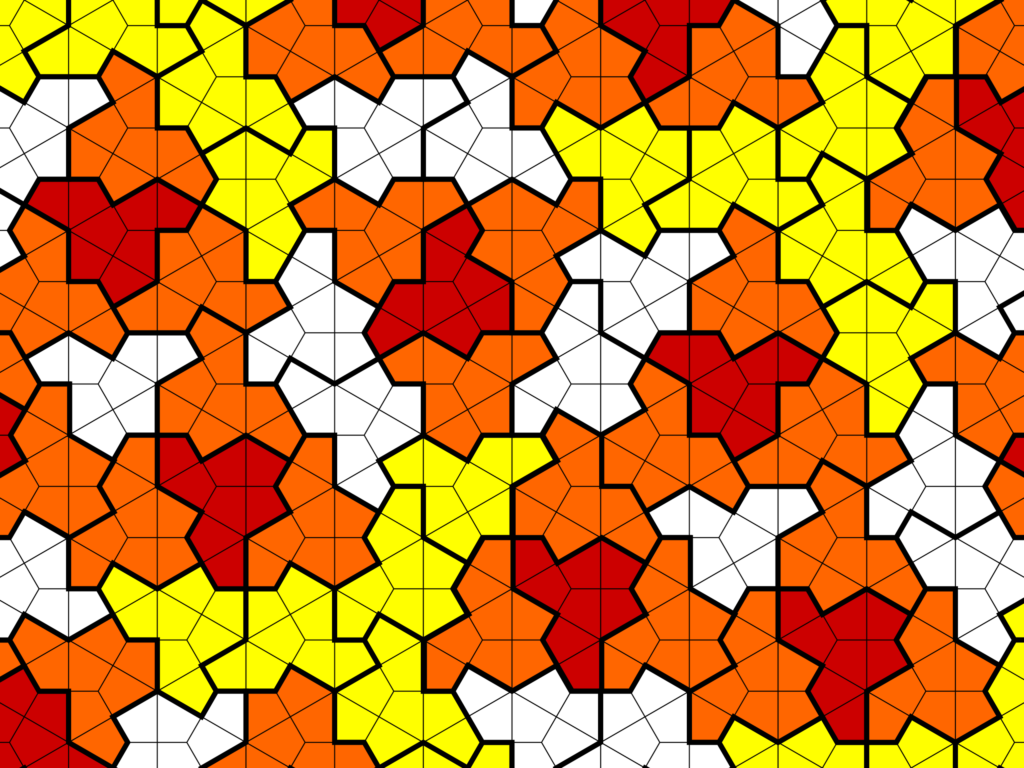
圖片來源:Wikipedia
這時史密斯又想出另一個形狀,看起來像是烏龜和帽子的混合體,也是13邊形,不過這次的組成不是箏形(如下圖)。這個形狀也可以做為愛因斯坦地磚,更讚的是完全不需要用到反面。

圖片來源:David Smith’s blog
只不過有個問題,如果搭配反面,反而可以排出規律的圖案(如下圖)。然而若按嚴格定義,愛因斯坦地磚只能有非週期性的排法,不允許還有規律的排法。

他們四人再次合作,很快地將找出方法,將直線的邊修改為曲線,如此便無法用正反面排出規律圖案,但仍能非週期性地密鋪整個平面(如頁首)。他們於五月發表論文,這個暱稱為「幽靈」(spectres) 的愛因斯坦地磚終於不會有人質疑了。
參考資料:











