二千三百年前如何知道太陽有多大?
我在2月19日那篇〈哥白尼冥誕〉中提到西元前二百多年的希臘學者阿里斯塔克斯(Aristarchus of Samos)推算出太陽的大小是地球的300倍。有讀者問道:他是怎麼推算的?
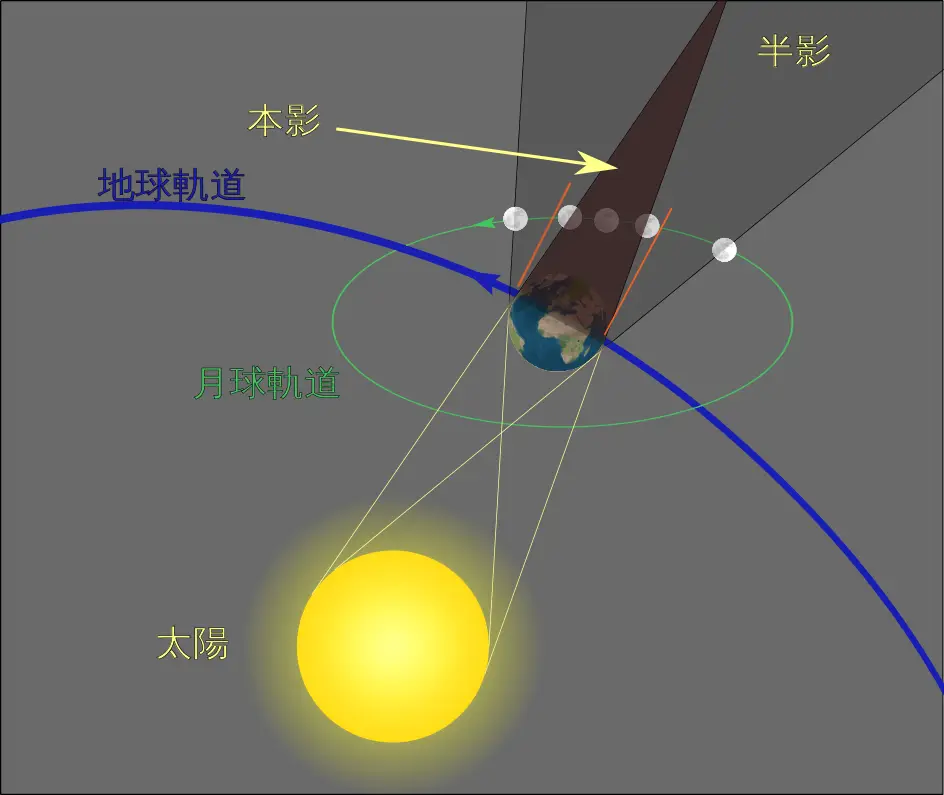
首先,阿里斯塔克斯在月全食時,從地球的影子剛好遮住一半月表時開始計時,直到月球完全被遮住後又冒出一半來,估算出地球的影子是月球直徑的2倍,因此地球直徑是月球的3倍。
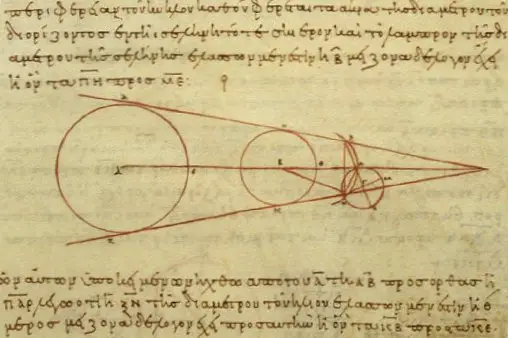
接著他知道上弦月和下弦月時,太陽、月球和地球的位置剛好是直角三角形,在量測出太陽和月球對地球的夾角為87°後,便可算出太陽到地球的距離是月球到地球的20倍(註)。
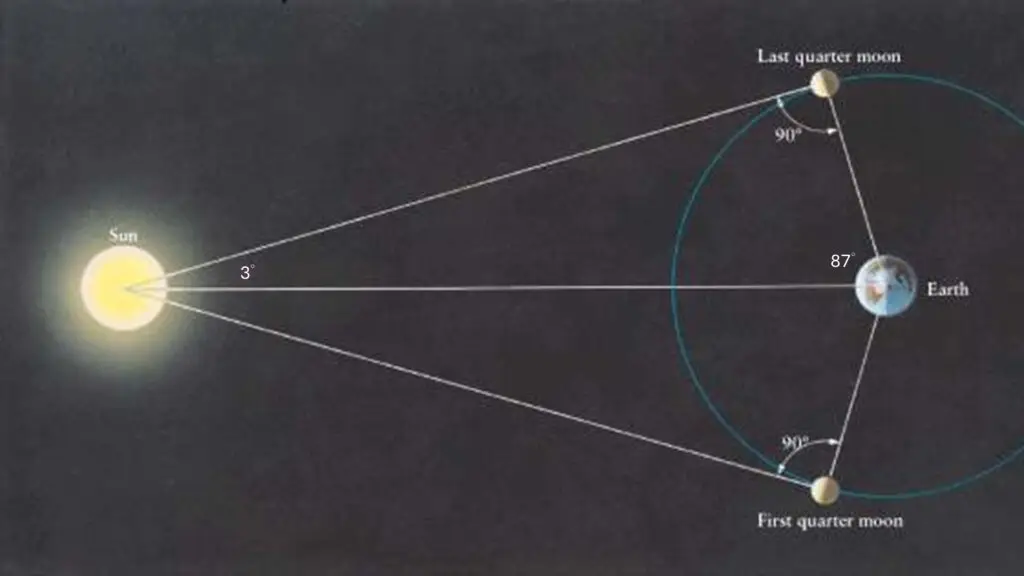
由於太陽和月球看起來一樣大,但太陽卻是20倍遠,代表太陽的直徑是月球的20倍大。而地球直徑是月球的3倍,因此太陽的直徑是地球的6.7倍,體積便是地球的300倍。
如今我們知道實際上地球直徑是月球的3.7倍,太陽的直徑則是地球的109倍,阿里斯塔克斯對月球的估算還可以,但太陽大小就差太多了。之所以如此,是因為太陽和月球對地球的夾角為89.5°,而他用87°去推算,雖然只差了2.5°,但隨著距離越遠,誤差便越來越大。
不過這也不能算是他的失誤,畢竟在尚無天文觀測器材的當時,他能估算出87°應該已是最佳表現了。撇開這個技術問題,阿里斯塔克斯從月食的成因、軌道運行,到幾何學的運用,都做出正確的推理,而這也充分展現了科學思維如何突破時代的限制,成為文明推進的重要力量。
另一位古希臘學者也憑藉抽象推理,在二千二百多年前就算出地球的大小,可參考我寫過的〈如果你在兩千多年前,如何知道地球大小?〉。
註:當時還沒有三角學,所以阿里斯塔克斯並不是直接用角度度數和三角函數來計算,而是根據角度和直角相差1/30(尚不清楚他是用觀測或用推算得知的),再用幾何方法算出太陽到地球的距離,是月球到地球的18到20倍之間。
參考資料: