今年諾貝爾物理獎頒給阿斯佩 (Alain Aspect)、克勞澤 (John F. Clauser) 與塞林格 (Anton Zeilinger) 三人,以表彰他們透過光子纏結實驗證明貝爾不等式不成立,以及率先研究量子資訊科學。很多人看到這幾個名詞都不知道是什麼意思,新聞報導也是有看沒懂,因此我想就來試試給個大家看得懂的解釋,並交代一下歷史脈絡。
一、 量子是什麼?
這得從「光究竟是粒子或波?」這個吵了幾百年的問題談起。原先是牛頓的粒子說居於上風,但兩百年後馬克士威提出電磁波理論,並經赫茲以實驗證明光是一種電磁波後,光波說又成為主流。但有個「黑體輻射」的問題(註 1)用光波說始終無法解釋,直到 1900 年普朗克提出「光量子」說,主張光的能量有最小基本單位,這個問題才獲得解決。
光有最小基本單位,不就代表光是粒子嗎?光波派怎能接受!不過愛因斯坦卻又用光子成功解釋「光電效應」(註 2),最後大家終於在 20 世紀初取得共識,光既是粒子也是波,具有「波粒二象性」。
沒想到過沒多久,德布羅意提出了「物質波」理論,主張電子、質子這些粒子也可以看成波,並且很快地獲得實驗證實,從此這些可以觀察到波粒二象性的微小粒子就概稱為「量子」,而描述它們特性與行為的理論就稱為量子理論或量子力學。
註 1:簡單說,光如果是電磁波,那麼物體加熱後應該會輻射出各種頻率的光,包括致命的紫外光。但顯然實際上並非如此。
註 2:光打在金屬表面會激發出電子,產生電流。但當時覺得很奇怪:為什麼低於某個頻率的光,強度再強也無法激發多電子?
二、 疊加態
光和各種基本粒子都是量子,具有波粒二象性,其中光波適用於馬克士威方程組,那麼物質波呢?
1926 年,薛丁格提出波動方程式,各種粒子終於也可以用波函數來描述。不料就在大家讚嘆之餘,玻恩 (Max Born) 竟跳出來語出驚人地說:
「你們都搞錯了,那個波函數不是代表真的波,而是一種機率波。」
「機率?」
「是的,粒子本身並沒有確切的狀態,而是由所有可能的狀態疊加在一起。你以為原子裡的電子一直乖乖的待在自己的軌道域裡嗎?不,它們就像包覆著原子核的一團雲,什麼位置都有可能,沒有界限。」
「胡說八道,粒子明明就在那裡,每次測到的各種數值都一樣,怎麼會沒有確切的狀態?」
「哈哈,那是因為我們對它進行觀測時,粒子才從具有各種可能性的「疊加態」崩陷為其中一種狀態。」
這下量子陣營炸鍋了,從此分為以玻恩、波耳、海森堡等人為首的「哥本哈根學派」,主張並沒有客觀實在、一切不過是測量的結果;以及由愛因斯坦領軍,堅信有客觀實在、無關乎觀不觀測的古典陣營。(順帶一提,大家應該都聽過「薛丁格的貓」這個思想實驗,但薛丁格可是在古典陣營這邊的,他也不相信有疊加態,才故意舉既生又死的貓為例,來嘲諷哥本哈根學派。)

三、不確定性原理
哥本哈根學派的主張看似荒誕不經,卻又無法證明是錯的,尤其海森堡於 1927 年提出的「測不準原理」,更是吻合許多粒子物理的實驗結果。根據海森堡的計算,我們無法同時知道粒子的確切位置和動量(以防有人你忘了,動量等於質量乘以速度);當你想越精準地測量它的位置,所測得的動量誤差就越大,反之亦然。總之位置的誤差與動量的誤差兩者相乘,一定會大於等於某個值,因此就像蹺蹺板一樣,一個誤差越小,另一個誤差就越大。
(其實測不準原理應該翻譯成不確定性原理才對,因為測不準會讓人以為是量測技術的問題,但哥本哈根學派根本就認為不確定性是粒子的本質,並非受限於量測技術所致。)
愛因斯坦決定從不確定性原理展開攻擊,只要找出同時測得粒子的位置與動量的方法,推翻不確定性原理,至少就能證明哥本哈根派的主張是不完備的。
於是愛因斯坦展開他最擅長的思想實驗,舉出同時測得位置與動量的方法,但波耳很快就發現其中漏洞,指出他所設想的機關會影響整體系統,因此還是測不準。愛因斯坦只好再構思另一種方法,卻又被波耳駁倒,如此數度攻防,不確定性原理始終屹立不搖,古典派只能暫時偃旗息鼓。
四、EPR悖論與量子纏結
1935年,愛因斯坦與另兩位物理學終於想出一個無懈可擊的方法:根據動量守恆原理,A、B 兩個粒子產生交互作用的前後,動量總和不會改變,因此在它們交互作用後測量 A 粒子的動量,就能推算出 B 粒子的動量。為了避免對 A 粒子的測量影響到 B 粒子,我們可以等到它們相距很遠,例如超過光速一秒所走的距離,再進行測量;而在此同時,也測量 B 粒子的位置。
既然光速不可能被超越已是公認的定理,那麼任一邊的測量結果絕對沒受到另一邊的影響,也就是說 B 粒子當下的動量與位置確實可以得知,但哥本哈根學派的量子理論卻無法同時表述出這兩個物理量的值,可見它並不完備。
好吧,那你說我們的理論不完備,但以機率和疊加態來詮釋波函數明明不斷獲得驗證,又怎麼說呢?愛因斯坦認為哥本哈根詮釋看似神奇,其實只是有某種「隱變數」我們還不知道,一旦把這尚未發現的隱變數納入古典理論,就會證明這世界確實是一種客觀的存在,而不是隨觀測而變。這就像以前會覺得磁力很神奇,但後來用電磁理論就能輕易解釋了。
薛丁格讀了愛因斯坦這篇論文後,拍案叫絕,並用「量子纏結」這個名詞稱呼這兩個產生交互作用的粒子。他進一步指出哥本哈根詮釋的荒謬之處:如果測量 A 粒子才讓它從疊加態崩陷為某一特定狀態,它的動量也就確定了;但根據動量守恆定律,B 粒子的動量在此瞬間也就確定下來。為什麼對 A 粒子進行測量的這個動作,會瞬間讓 B 粒子從疊加態崩陷為確定狀態。尤其若依愛因斯坦等人的思想實驗所說的,等到兩個粒子相距甚遠才測量 A 粒子,怎麼可能會有超越光速的神祕力量,讓 B粒子「知道」應該變成與 A 粒子相符的狀態?愛因斯坦聞之也附和嘲笑說這根本是「鬼魅的超距作用」。
愛因斯坦與另兩位物理學家的這個思想實驗從此便以「EPR悖論」著稱(EPR分別是他們三人姓氏的第一個字母),而這一次哥本哈根派就找不出漏洞,無法反駁。問題是,EPR 悖論在真正進行實驗之前,只能算是合理的推論,不能就此判定哥本哈根學派的學說有問題,更何況各項實驗結果也一直都符合他們的理論預測。
因此 EPR 悖論只是一道防線,暫時守住古典派的陣地,不讓哥本哈根學派席捲一切。雙方就這麼僵持近三十年後,古典派一位沒沒無聞的新生代宣稱找到了反攻之道,因為他已經想出如何驗證 EPR 悖論的方法……。
五、貝爾其人
想像有個來自哥本哈根的魔術師將兩枚硬幣分別放進兩個盒子裡,再將它們旋轉後蓋上盒子,然後預言打開盒子後,看到的兩枚硬幣絕對是一正一反朝上。
他請兩名觀眾上台各自打開一個盒子,果真一枚硬幣人頭朝上,另一枚反面朝上。為了證明這不是巧合而且沒動手腳,魔術師退到一旁,讓觀眾自己準備硬幣和盒子,由觀眾旋轉硬幣再分別放進盒子後,拿到劇院外再打開,很奇妙地仍是如此,換誰來試幾次也都一樣,屢試不爽。
魔術師發誓絕對沒有作弊,而他也不知道為什麼會這樣,只是發現兩枚硬幣一起旋轉後,似乎就產生了奇妙的連結,能感應到對方的行為來決定自己應該如何表現。但一群來自古典學園的觀眾打死不信,認為背後一定隱藏著什麼機關(隱變數),只要找出這機關就會恍然大悟,發現這魔術一點也不神祕。
數十年過去,這群古典學園的觀眾逐漸凋零,卻始終無法找到背後的機關,而這魔術師卻越來越受歡迎,受到各地觀眾的擁戴。不過在人數稀疏的古典派團員中,仍有位年輕觀眾暗自立誓要拆穿這魔術……。

貝爾 (John S. Bell) 出生於北愛爾蘭,1956 年拿到博士學位,研究領域是核子物理與量子場論。就學期間,他發現哥本哈根學派儼然成為量子物理的正統,所謂的量子論已變成指的是哥本哈根學派的理論,這令他難以接受,因為他心中是偏向古典陣營這邊的。愛因斯坦就在他獲得博士學位前一年過世,一代宗師已去,他更想證明愛因斯坦是對的,一定有某種隱變數可以解釋奇特的量子現象,不需要哥本哈根詮釋。
貝爾先在英國原子能研究所上班,四年後轉往歐洲核子研究組織 (CERN),憑藉自己的專長參與粒子加速器的設計工作。閒暇時他一直思索如何進行 EPR 實驗,證明纏結的兩顆粒子在分開後,其狀態就已經確定了,而不是處於疊加態中,直到觀測才有確定的狀態。
經過多年的思索後,貝爾終於在 1964 年想出驗證 EPR 悖論的方法:只要多次測量兩顆纏結粒子的自旋方向,然後統計它們的相關性。
六、自旋方向和相關性
電子有自旋向上和自旋向下兩種方向,雖然實際上電子自旋並不是像地球那樣自轉,但方便起見,你就暫且這麼想像,然後用右手法則,四根手指代表電子旋轉方向;逆時鐘轉,拇指向上就是自旋方向,反之,順時鐘就是自旋向下。
產生纏結的電子對自旋方向剛好彼此相反,一個向上,另一個就是向下,這種絕對不變的關係類似動量守恆,便可以用在 EPR 實驗中。等等,你說電子的自旋方向一上一下在分開前就確定了,但是哥本哈根學派還是可以主張在測量之前,它們各自的自旋方向仍處於向上和向下的疊加態,直到測量那一瞬間才確定下來,這樣還是各說各話,無從驗證孰是孰非啊。
沒錯,所以還需要利用相關性來做區分。
相關性就是兩個變數或事件的相關程度,像身高和體重有很高的相關性,但身高和考試成績就沒什麼相關性;還有一種剛好相反的則是負相關,例如氣溫越高,電暖器越賣不出去,氣溫和電暖器銷量就是負相關。如果百分之百一定會伴隨著發生的,相關性為 +1,完全沒相關的相關性為 0,而一個發生、另一個絕對不會發生的相關性則是 -1。所以產生纏結的 A 電子自旋向上, B 電子自旋向下,兩者的相關性就是 +1,而兩者都自旋向上或是都自旋向下的相關性就是 -1。
好了,接下來可以看看貝爾的巧思了。
七、貝爾不等式
我們再借用前面硬幣魔術的例子,人頭向上就代表電子自旋向上,反面就代表自旋向下。現在貝爾向魔術師提出挑戰:
「你可以讓硬幣停止旋轉時不會倒下來嗎?」
魔術師想了想後,回說:「可以,但這樣硬幣不就都是邊緣向上嗎?」
「所以得從盒子側面打開,才能看見硬幣是哪一面。不過我希望改成像比薩盒那樣,但不是正方形,而是圓形。比薩盒上方的蓋子像時鐘那樣標示 1 到 12 ,然後每個數字的側邊有個小窗口,觀眾各選一個窗口打開後,回報看見硬幣哪一面。」
「萬一剛好硬幣邊緣正對自己呢?」
「那就觀眾自己決定是正面或反面。此外觀眾也不是隨意選窗口,而是從你指定的三個窗口中選一個,不過兩人不能選一樣的,例如你指定 12、3、8 的話,他們所選的組合就只有 (12, 3)、(12, 8)、(3, 8) 三種。」
魔術師眉頭一揚,不懂貝爾這項要求的用意。
貝爾繼續解釋:「這是為了比較相關性的差異。」
「相關性?」
「是的,你之前的表演,兩枚硬幣總是一正一反,所以相關性是 +1。現在我這個方式,硬幣邊緣有時可能介於兩名觀眾所選的窗口之間,這種情況下,兩人回報的會是同一面,計算相關性時以 -1 計,相關性的平均值就會小於 1。而如果兩個開口相差的角度超過 90 度,多數的情況反而是兩人看到同一面,此時相關性就變負的了。」
「這我明白,但我不懂相關性又能證明什麼。」
此時貝爾推出黑板,在上面邊寫邊說:「如果真相是如我們古典派所主張的,兩枚硬幣在盒子打開前就已確定朝向哪裡,那麼相關性就只取決於硬幣的方向和開口的角度。拿開口是 (12, 3) 為例,相關性是 -1*1/2 + 1*/2 = 0(如圖,硬幣邊緣從 12 點鐘到 3 點鐘位置,以及 6 點鐘到 9 點鐘位置,兩個開口會在硬幣不同側,機率是 1/2);(12, 8) 的相關性是 -1*8/12 + 1*4/12 = -1/3;(3, 8) 的相關性是 -1*10/12 + 1*2/12 = -2/3。」

「所以呢?」魔術師已經開始不耐煩。
「我算過了,假定 x、y、z 代表你指定的三個窗口,然後用 Pxz、Pzy 和 Pxy 分別表示它們兩兩之間的相關性,那麼無論這三個窗口之間的夾角是多少,都會符合這條不等式!」貝爾在黑板用力寫下:
|Pxz – Pzy| ≦ 1 + Pxy
魔術師恍然大悟:「我明白了!相反地,如果我所說的都是真的,兩個硬幣彼此有神祕的連結,能感應對方來調整自己的表現,那麼相關性應該會更高。如此一來,你的不等式就不成立了,是吧?」
貝爾指著魔術師說:「沒錯,你既然宣稱沒有作弊,那就接受這個挑戰,進行我說的實驗吧!我雖然破解不了你的魔術手法,但我相信實驗結果一定會證明背後藏有某種機關(隱變數),根本沒有什麼纏結作用。」
魔術師笑笑說:「沒問題,不過我看你空手而來,想必也沒做出這樣的盒子吧?沒關係,我很樂意設法打造出來,到時候就按你說的來驗證這條不等式。但我相信結果恐怕會讓你期望落空啊,年輕人。」
八、驗證結果
實際要進行貝爾設想的實驗並不容易,直到 1972 年,美國物理學家克勞澤 (John F. Clauser) 和弗里德曼 (Stuart Freedman) 用纏結的光子,偵側其偏振方向,才首度實現貝爾不等式的測試。雖然實驗數據顯式貝爾不等式不成立,卻因光源強度不足,漏測了許多光子,加上觀測的距離仍不夠遠,無法完全排除有隱變數的作用,因此仍不算是有效證明。
十年之後,法國物理學家阿斯佩 (Alain Aspect) 以雷射光源產生的光子進行實驗,並讓偵測器相距 12 公尺,偵測方向每 10 奈秒隨機改變,由於光速在 10 奈秒內走不到 12 公尺,證明古典派聲稱的隱變數也不可能產生影響,終於毫無疑義地證明貝爾不等式不成立。不僅如此,實驗數據還完全符合量子理論所預測的相關性,將古典派徹底打垮。
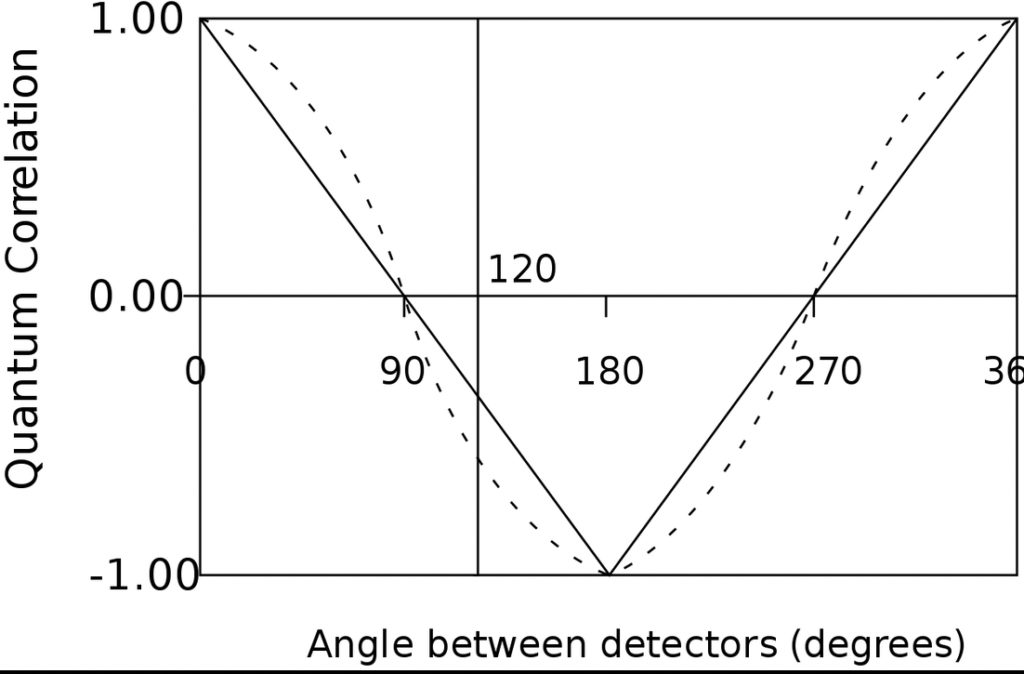
古典派即使仍不死心,要指阿斯佩的隨機改變偵測方向並非真的隨機,隱變數冥冥之中已預先影響了偵測方向的選擇,那麼 1998 年由奧地利物理學家塞林格 (Anton Zeilinger) 領軍的實驗,就讓隨機選擇徹底排除隱變數的可能影響,愛因斯坦的主張終於被宣判死刑了。
貝爾本想用貝爾不等式給予哥本哈根學派致命一擊,沒想到反而成為古典學派的輓歌。不過也因為他的「弄巧成拙」,才讓量子纏結的神奇作用獲得證實,同時促成量子計算、量子通訊等應用,貢獻厥偉。據說他 1990 年就獲得諾貝爾物理獎的提名,可惜他當年 10 月 1 日就腦溢血死亡,無緣獲獎。如果他能活到今日(94歲雖然算是稀壽,但也不無可能),今年的諾貝爾物理獎應該會有他一份吧。
參考資料:










