愛因斯坦的諾貝爾獎金全給了前妻，但她還是失去了一切
1922年，愛因斯坦終於獲得早該得到的諾貝爾物理學獎。不過，獎金卻全部給了前妻米列娃，因為他10年前就變心，為了要求離婚，便提出這張未來的支票做為贍養費。
瑞棋 張
愛因斯坦拿到諾貝爾獎的一波三折
愛因斯坦獲得1921年的諾貝爾物理學獎，得獎原因卻不是最具革命性的相對論。而且諾貝爾獎委員會直到1922年才宣布，然後愛因斯坦直到1923年才拿到獎章，這是怎麼回事？
駁斥不成變助攻——密立根的光電效應實驗
愛因斯坦於1905年發表論文，提出光量子的概念，成功解釋困擾科學家很久的光電效應。不過密立根不以為然，他著手進行實驗，要證明光量子假說是錯的，沒想到卻適得其反……。
光量子現身——愛因斯坦的光電效應論文
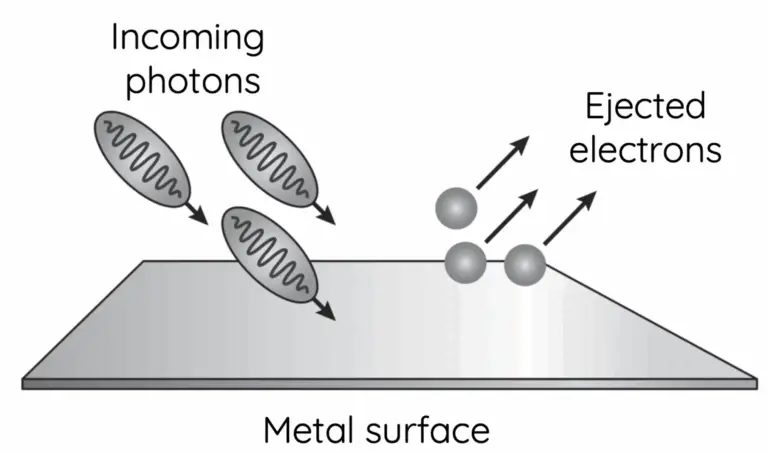
名聞遐邇的愛因斯坦，終於在1921年獲得諾貝爾物理學獎，不過獲獎的具體理由卻與狹義相對論或廣義相對論都沒關係，而是他發現了光電效應的物理定律。
6月5日—發明全像攝影的人
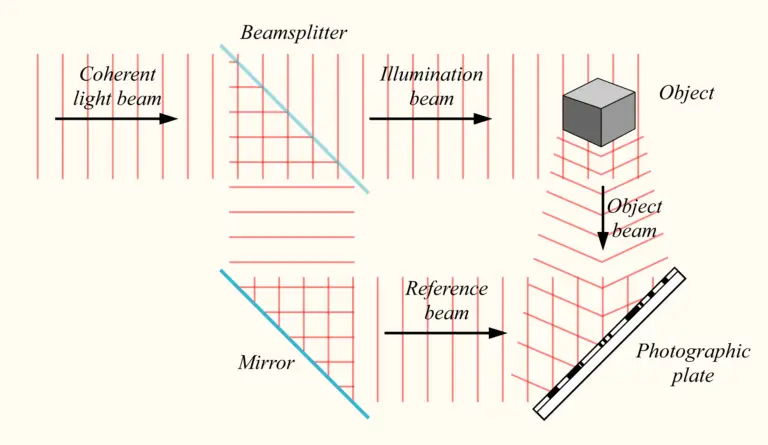
神奇的是，一般攝影只能拍下物體的單一角度，全像攝影卻能計算出各個角度，因此可以呈現出物體的三維影像。而且即使全像底片碎裂成許多小碎片，我們仍能任憑其中一小片，絲毫不差地還原出完整的樣貌。