換？不換？——蒙地霍爾問題

元宵節猜燈謎，若要應景，我想到的是之前在科學史上的今天寫過的「蒙地霍爾問題」。

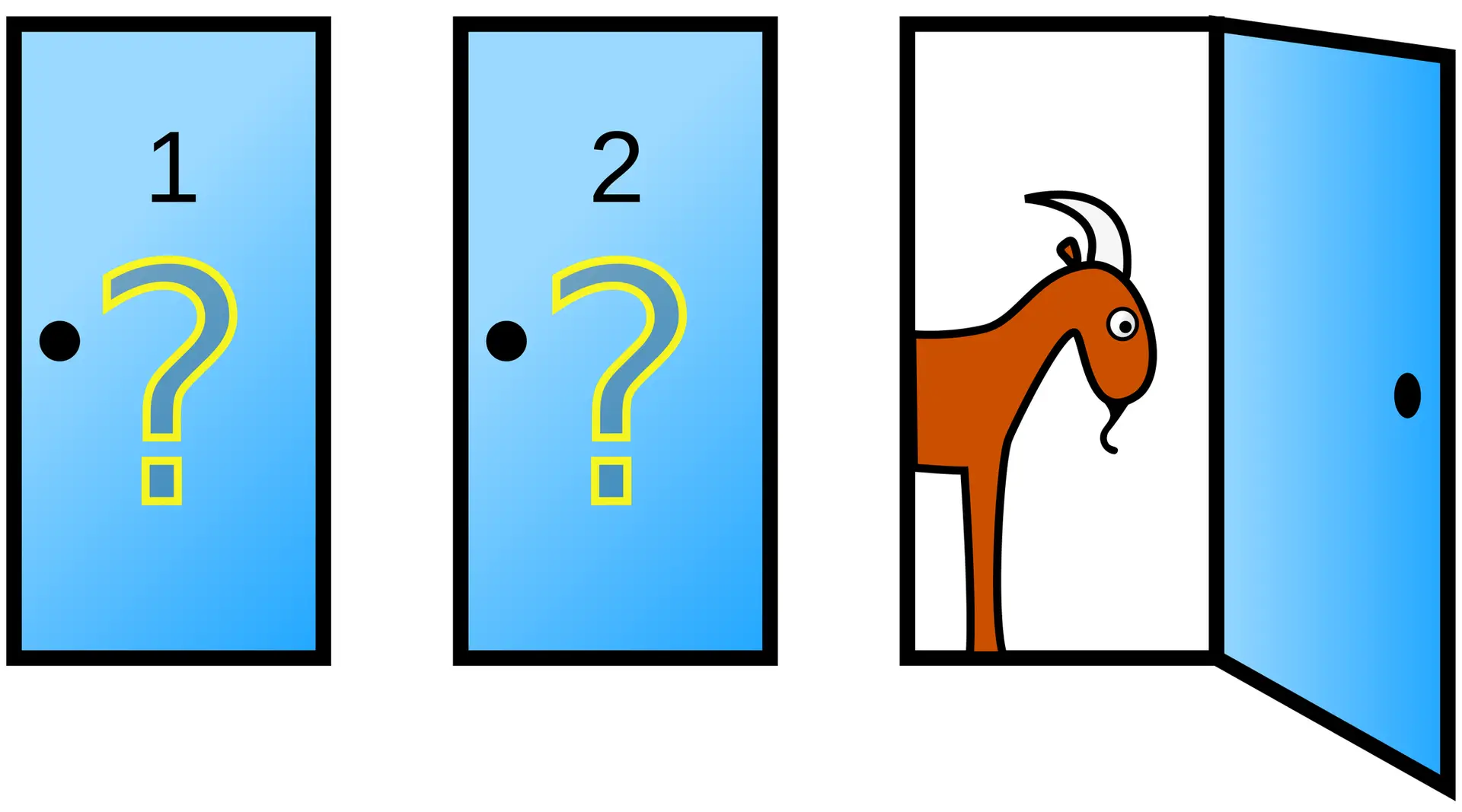
想像你參加美國益智電視節目「做個交易吧」（Let’s Make a Deal），幸運地過關斬將，來到最後一關。在你眼前有三道門，你可以任選一道，門後的東西就是你的。有一道門後是最大獎汽車一部，另外兩道門則各是一頭山羊。

你憑直覺選了其中一扇門，知道門後藏了什麼的主持人蒙地·霍爾（Monty Hall）走到你沒選的另兩扇門中的一個，緩緩地打開────是頭山羊。你鬆了一口氣，此時霍爾卻以神秘的笑容問你：「再給你一次機會，要不要換另一扇門？」

你該堅持原來的選擇，還是該換另一扇門？

1990 年 9 月 9 日，莎凡特（Marilyn vos Savant）在雜誌專欄上回答了這個問題：應該換，因為換了，選到汽車的機率就會從 1/3 提高到 2/3。

莎凡特 10 歲時測得的智商高達 228，是金氏世界紀錄的保持人（但這個項目在 1990 年後就廢除了），她自 1986 年起在《Parade》雜誌開闢「請問瑪莉蓮」專欄，專門回答讀者帶有科學或數學成份的生活問題，相當受到歡迎。

沒想到，她這個回答引來數以千封的抗議信件，讀者們不解向來令人信服的瑪莉蓮為何會犯下如此初級的錯誤。不就剩兩扇門沒打開嘛，不論換不換，輸贏的機會都各半，怎麼會一扇門的勝算是另一扇門的兩倍？來信中更不乏博士級的讀者指責她搞砸了，要她先去上機率的課程。

莎凡特只好在下一期的專欄中列出所有可能性的樣本空間，以證明自己所言無誤，但還是有不少讀者不肯相信，繼續來信抨擊她：「已經有三位數學家指正你了，你還不承認錯誤？！」莎凡特沒有再花力氣在數學上，而是呼籲學校老師在班上實際做實驗看看。結果超過一千個班級做了實驗，幾乎百分之百證實換比不換好；有許多人用電腦模擬也都證明如此。

有趣的是，連大數學家艾狄胥（Paul Erdős）也都搞錯，甚至看了同事的證明仍不肯相信，直到幾百次的電腦模擬顯示換的勝算是 2/3 後，他才承認自己的直覺是錯的。

正如葛登能（Martin Gardner）在《科學美國人》轉載這個「蒙地霍爾問題」時所下的註解：「數學中還沒有其它哪個領域，比機率理論更容易令專家出錯。」

如果你仍難以接受這個答案，有個思考方式或許可以幫你搞清楚。

換的結果是好是壞，其實取決於你一開始的選擇，是吧？如果你原本沒選到汽車那扇門（這樣的機率是 2/3），那麼換了就能得到汽車；除非你很幸運一開始選到汽車（這樣的機率是 1/3），換了才反而不好。既然前者發生的機率比較大，當然換的勝率會比較高。

後記：

不過這個問題如果改從行為經濟學的角度來看，換不換對參賽者的感受而言，可能就都沒差囉。為什麼？請看下一篇〈蒙地霍爾問題的另一解——展望理論〉。